A fully differentiable geothermal doublet: History matching and control optimization

Geothermal   StartToFinish   Advanced   HistoryMatching   Optimization   Differentiability  

We are going to set up a conceptual geothermal doublet model in 2D and perform gradient based history matching. This example serves two main purposes:

1. It demonstrates the conceptual workflow for setting up a geothermal model from scratch with a fairly straightforward mesh setup.

2. It shows how to set up a gradient based history matching workflow with the generic optimization interface that allows for optimizing any input parameter used in the setup of a model.

Load packages and define units

using Jutul, JutulDarcy, HYPRE, GLMakie
meter, kilogram, bar, year, liter, second, darcy, day = si_units(:meter, :kilogram, :bar, :year, :liter, :second, :darcy, :day)

(1.0, 1.0, 100000.0, 3.1556952e7, 0.001, 1.0, 9.86923266716013e-13, 86400.0)

Set up the reservoir mesh

The model is a typical geothermal case where there is a layer of high permeability in the middle, confined between two low-permeable layers. For a geothermal model, the low permeable layers are important, as they store significant amounts of heat that can be conducted to the high permeable layer during production.

We set up the mesh so that the high permeable layer where most of the advective transport occurs has a higher lateral resolution than the low permeable layers. The model is also essentally 2D as there is only one cell thickness in the y direction - a choice that is made to make the example fast to run, especially during the later optimization stages where many simulations must be run to achieve convergence.

nx = 50
ntop = 5
nmiddle = 10
nbottom = 5
nz = ntop + nmiddle + nbottom

20

Set up layer thicknesses and vertical cell thicknesses

top_layer_thickness = 300.0*meter
middle_layer_thickness = 200.0*meter
bottom_layer_thickness = 300.0*meter
dz = Float64[]
for i in 1:ntop
    push!(dz, top_layer_thickness/ntop)
end
for i in 1:nmiddle
    push!(dz, middle_layer_thickness/nmiddle)
end
for i in 1:ntop
    push!(dz, bottom_layer_thickness/nbottom)
end

cmesh = CartesianMesh((nx, 1, nz), (2000.0, 50.0, dz))
rmesh = UnstructuredMesh(cmesh, z_is_depth = true)

UnstructuredMesh with 1000 cells, 1930 faces and 2140 boundary faces

Define regions based on our selected depths

We tag each cell with a region number based on its depth. The top layer is region 1, the middle layer is region 2, and the bottom layer is region 3.

geo = tpfv_geometry(rmesh)
depths = geo.cell_centroids[3, :]
regions = Int[]
for (i, d_i) in enumerate(depths)
    if d_i <= top_layer_thickness
        r = 1
    elseif d_i <= top_layer_thickness + middle_layer_thickness
        r = 2
    else
        r = 3
    end
    push!(regions, r)
end

Plot the mesh and regions

fig, ax, plt = plot_cell_data(rmesh, regions,
    alpha = 0.5,
    outer = true,
    transparency = true,
    colormap = Categorical(:heat)
)
ax.elevation[] = 0.0
ax.azimuth[] = π/2
plot_mesh_edges!(ax, rmesh)
fig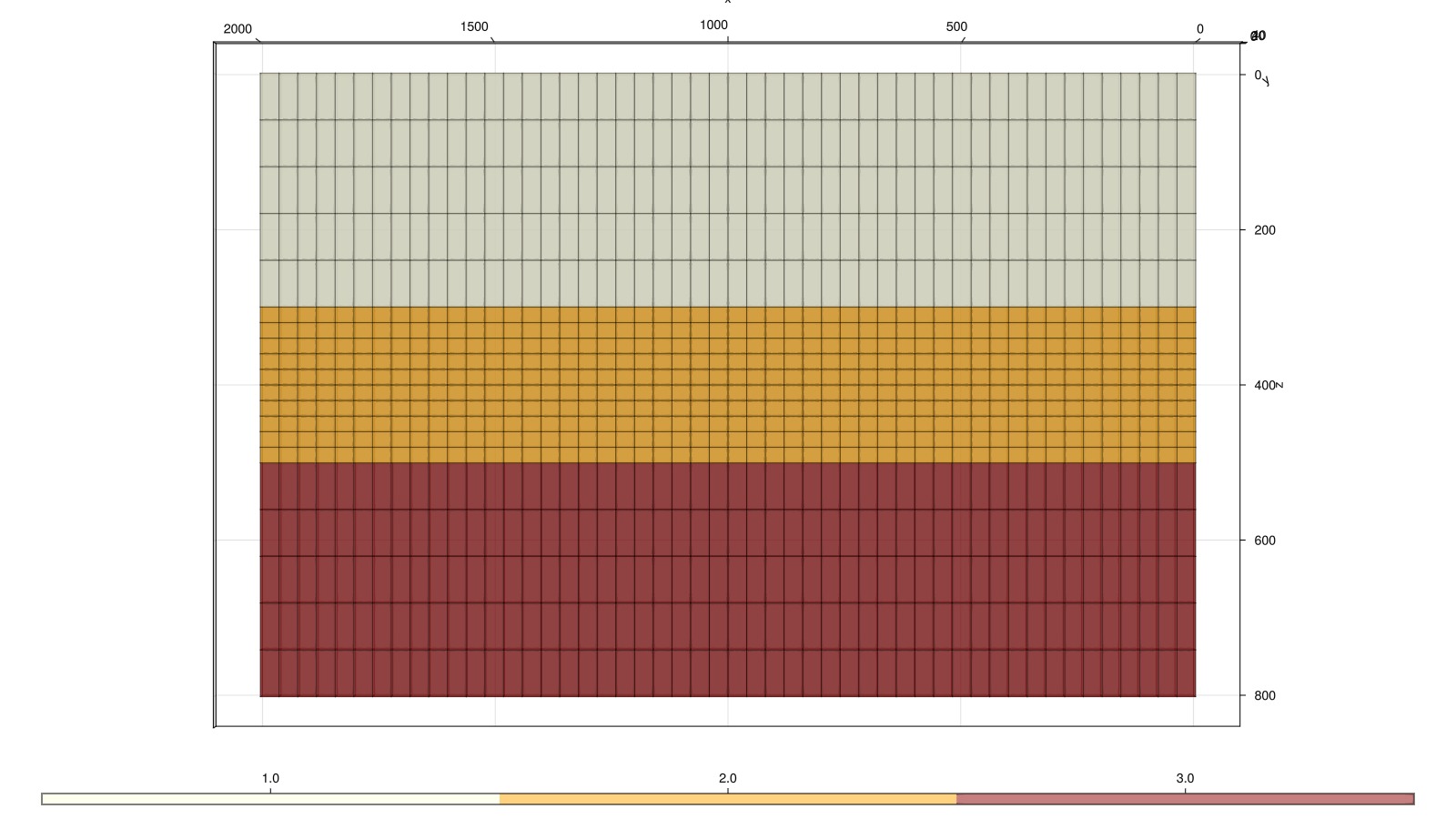

Define functions for setting up the simulation

We will define a function that takes in a Dict with different values and sets up the simulation. The key idea is that we can then optimize the values in the Dict to perform optimization. As we can define any such Dict to set up the model, this interface is very flexible and can be used for both control optimization and history matching with respect to almost any parameter of the model. The disadvantage is that the setup function will be called many times, which can be a substantial cost compared to the more structured optimization interface that only allows for optimization of the numerical parameters (e.g. for the CGNet example).

Define the time schedule

We set up a time schedule for the simulation. The total simulation time is 30 years, and we report the results every 120 days. We also define ten different intervals in this 30 year period, which are the period where we will allow the rates and temperatures to vary during the last part of the optimization tutorial.

total_time = 30.0*year
report_step_length = 120.0*day
dt = fill(report_step_length, Int(ceil(total_time/report_step_length)))
num_intervals = 10
interval_interval = total_time/num_intervals
interval_for_step = map(t -> min(Int(ceil(t/interval_interval)), num_intervals), cumsum(dt))

92-element Vector{Int64}:
  1
  1
  1
  1
  1
  1
  1
  1
  1
  2
  ⋮
 10
 10
 10
 10
 10
 10
 10
 10
 10

Define the wells

We set up two wells, one injector and one producer. The injector is located at the left side of the model, and the producer is located at the right side. We use multisegment wells.

base_rate = 15*liter/second
base_temp = 15.0

domain = reservoir_domain(rmesh)
inj_well = setup_vertical_well(domain, 5, 1,
    heel = ntop+1,
    toe = ntop+nmiddle,
    name = :Injector,
    simple_well = false
)
prod_well = setup_vertical_well(domain, nx - 5, 1,
    heel = ntop+1,
    toe = ntop+nmiddle,
    name = :Producer,
    simple_well = false
)

model_base = setup_reservoir_model(
    domain, :geothermal,
    wells = [inj_well, prod_well],
);

Set up a helper to define the forces for a given rate and temperature

function setup_doublet_forces(model, inj_temp, inj_rate)
    T_Kelvin = convert_to_si(inj_temp, :Celsius)
    rate_target = TotalRateTarget(inj_rate)
    ctrl_inj  = InjectorControl(rate_target, [1.0],
        density = 1000.0, temperature = T_Kelvin)

    bhp_target = BottomHolePressureTarget(50*bar)
    ctrl_prod = ProducerControl(bhp_target)

    control = Dict(:Injector => ctrl_inj, :Producer => ctrl_prod)
    return setup_reservoir_forces(model, control = control)
end

setup_doublet_forces (generic function with 1 method)

Define the main setup function

This function sets up the model based on the parameters provided in the Dict. It takes in two arguments: The required parameters in a Dict and an optional step_info argument that can be used to set up the model for a specific time step. The function returns a JutulCase object that can be used to simulate the reservoir. Here, we ignore the step_info argument and set up the entire schedule every time. Jutul will then automatically use the correct force based on the time step in the simulation.

function setup_doublet_case(prm, step_info = missing)
    model = deepcopy(model_base)
    rdomain = reservoir_domain(model)
    rdomain[:permeability] = prm["layer_perm"][regions]
    rdomain[:porosity] = prm["layer_porosities"][regions]
    rdomain[:rock_heat_capacity] = prm["layer_heat_capacity"][regions]

    T0 = convert_to_si(70, :Celsius)
    thermal_gradient = 20.0/1000.0*meter
    eql = EquilibriumRegion(model, 50*bar, 0.0, temperature_vs_depth = z -> T0 + z*thermal_gradient)
    state0 = setup_reservoir_state(model, eql)

    forces_per_interval = map((T, rate) -> setup_doublet_forces(model, T, rate),
        prm["injection_temperature_C"], prm["injection_rate"])

    forces = forces_per_interval[interval_for_step]

    return JutulCase(model, dt, forces, state0 = state0)
end

setup_doublet_case (generic function with 2 methods)

Perform a history match

We first set up a truth case that we will use to generate the data for the history match. We define high perm and porosity in the middle layer, and low perm and porosity in the top and bottom layers before simulating the model.

prm_truth = Dict(
    "injection_rate" => fill(base_rate, num_intervals),
    "injection_temperature_C" => fill(base_temp, num_intervals),
    "layer_porosities" => [0.1, 0.3, 0.1],
    "layer_perm" => [0.01, 0.8, 0.02].*darcy,
    "layer_heat_capacity" => [500.0, 600.0, 450.0], # Watt / m K
)
case_truth = setup_doublet_case(prm_truth)
ws, states = simulate_reservoir(case_truth)

ReservoirSimResult with 92 entries:

  wells (2 present):
    :Producer
    :Injector
    Results per well:
       :lrat => Vector{Float64} of size (92,)
       :wrat => Vector{Float64} of size (92,)
       :temperature => Vector{Float64} of size (92,)
       :control => Vector{Symbol} of size (92,)
       :Aqueous_mass_rate => Vector{Float64} of size (92,)
       :bhp => Vector{Float64} of size (92,)
       :wcut => Vector{Float64} of size (92,)
       :mass_rate => Vector{Float64} of size (92,)
       :rate => Vector{Float64} of size (92,)
       :mrat => Vector{Float64} of size (92,)

  states (Vector with 92 entries, reservoir variables for each state)
    :Pressure => Vector{Float64} of size (1000,)
    :TotalMasses => Matrix{Float64} of size (1, 1000)
    :TotalThermalEnergy => Vector{Float64} of size (1000,)
    :FluidEnthalpy => Matrix{Float64} of size (1, 1000)
    :Temperature => Vector{Float64} of size (1000,)
    :PhaseMassDensities => Matrix{Float64} of size (1, 1000)
    :RockInternalEnergy => Vector{Float64} of size (1000,)
    :FluidInternalEnergy => Matrix{Float64} of size (1, 1000)

  time (report time for each state)
     Vector{Float64} of length 92

  result (extended states, reports)
     SimResult with 92 entries

  extra
     Dict{Any, Any} with keys :simulator, :config

  Completed at Mar. 10 2026 09:02 after 4 seconds, 658 milliseconds, 471.2 microseconds.

Define a mismatch objective function

The mismatch objective function is defined as the sum of squares difference between the simulated values and the reference values observed in the wells. Note that we only make use of the well data:

• The temperature at the producer well

• The mass rate at the producer well (since it is controlled on BHP)

• The BHP at the injector well (since it is controlled on rate)

We use the get_1d_interpolator function to create interpolators for the reference values, since we cannot assume that the simulator will use exactly the same time-steps as the reference values.

prod_rate = ws.wells[:Producer][:wrat]
prod_temp = ws.wells[:Producer][:temperature]
inj_bhp = ws.wells[:Injector][:bhp]

prod_temp_by_time = get_1d_interpolator(ws.time, prod_temp)
prod_rate_by_time = get_1d_interpolator(ws.time, prod_rate)
inj_pressure_by_time = get_1d_interpolator(ws.time, inj_bhp)

import JutulDarcy: compute_well_qoi
function mismatch_objective(m, s, dt, step_info, forces)
    current_time = step_info[:time]
    # Current values
    T_at_prod = compute_well_qoi(m, s, forces, :Producer, :temperature)
    rate = compute_well_qoi(m, s, forces, :Producer, :wrat)
    bhp = compute_well_qoi(m, s, forces, :Injector, :bhp)
    # Reference values
    T_at_prod_ref = prod_temp_by_time(current_time)
    rate_ref = prod_rate_by_time(current_time)
    bhp_ref = inj_pressure_by_time(current_time)
    # Define mismatch by scaling each term
    T_mismatch = (T_at_prod_ref - T_at_prod)
    rate_mismatch = (rate_ref - rate)*1000
    bhp_mismatch = (bhp - bhp_ref)/bar
    return dt * sqrt(T_mismatch^2 + rate_mismatch^2 + bhp_mismatch^2) / total_time
end

mismatch_objective (generic function with 1 method)

Pick an initial guess

We set up an initial guess for the parameters that we will optimize. We assume the injection rate and temperature to be known and we set the porosities and permeabilities to uniform values. The heat capacity is given a bit of layering, but still with completely wrong values.

prm_guess = Dict(
    "injection_rate" => fill(base_rate, num_intervals),
    "injection_temperature_C" => fill(base_temp, num_intervals),
    "layer_porosities" => [0.2, 0.2, 0.2],
    "layer_perm" => [0.2, 0.2, 0.2].*darcy,
    "layer_heat_capacity" => [400.0, 400.0, 400.0]
)
case_guess = setup_doublet_case(prm_guess)
ws_guess, states_guess = simulate_reservoir(case_guess)

ReservoirSimResult with 92 entries:

  wells (2 present):
    :Producer
    :Injector
    Results per well:
       :lrat => Vector{Float64} of size (92,)
       :wrat => Vector{Float64} of size (92,)
       :temperature => Vector{Float64} of size (92,)
       :control => Vector{Symbol} of size (92,)
       :Aqueous_mass_rate => Vector{Float64} of size (92,)
       :bhp => Vector{Float64} of size (92,)
       :wcut => Vector{Float64} of size (92,)
       :mass_rate => Vector{Float64} of size (92,)
       :rate => Vector{Float64} of size (92,)
       :mrat => Vector{Float64} of size (92,)

  states (Vector with 92 entries, reservoir variables for each state)
    :Pressure => Vector{Float64} of size (1000,)
    :TotalMasses => Matrix{Float64} of size (1, 1000)
    :TotalThermalEnergy => Vector{Float64} of size (1000,)
    :FluidEnthalpy => Matrix{Float64} of size (1, 1000)
    :Temperature => Vector{Float64} of size (1000,)
    :PhaseMassDensities => Matrix{Float64} of size (1, 1000)
    :RockInternalEnergy => Vector{Float64} of size (1000,)
    :FluidInternalEnergy => Matrix{Float64} of size (1, 1000)

  time (report time for each state)
     Vector{Float64} of length 92

  result (extended states, reports)
     SimResult with 92 entries

  extra
     Dict{Any, Any} with keys :simulator, :config

  Completed at Mar. 10 2026 09:02 after 796 milliseconds, 357 microseconds, 799 nanoseconds.

Set up the optimization

We define a dictionary optimization problem that will optimize the parameters in the prm_guess dictionary. We start by setting up the object itself, which takes in the initial guess Dict and the corresponding setup function.

opt = JutulDarcy.setup_reservoir_dict_optimization(prm_guess, setup_doublet_case)

DictParameters with 5 parameters (0 active), and 0 multipliers:
No active optimization parameters.
Inactive optimization parameters
┌─────────────────────────┬──────────────────┬───────┬─────┬─────┐
│                    Name │ Initial value    │ Count │ Min │ Max │
├─────────────────────────┼──────────────────┼───────┼─────┼─────┤
│     layer_heat_capacity │ 400.0 ± 0.0      │     3 │   - │   - │
│          injection_rate │ 0.015 ± 3.47e-18 │    10 │   - │   - │
│ injection_temperature_C │ 15.0 ± 0.0       │    10 │   - │   - │
│              layer_perm │ 1.97e-13 ± 0.0   │     3 │   - │   - │
│        layer_porosities │ 0.2 ± 2.78e-17   │     3 │   - │   - │
└─────────────────────────┴──────────────────┴───────┴─────┴─────┘
No multipliers set.

Define active parameters and their limits

Note that while the parameters get listed, they are all marked as inactive. We need to explicitly make them free/active and specify a range for each parameter before we can optimize them. We use wide absolute limits for each entry.

free_optimization_parameter!(opt, "layer_perm", abs_max = 1.5*darcy, abs_min = 0.01*darcy)
free_optimization_parameter!(opt, "layer_heat_capacity", abs_max = 1000.0, abs_min = 400.0)
free_optimization_parameter!(opt, "layer_porosities", abs_max = 0.35, abs_min = 0.05)

DictParameters with 5 parameters (3 active), and 0 multipliers:
Active optimization parameters
┌─────────────────────┬────────────────┬───────┬──────────┬──────────┐
│                Name │ Initial value  │ Count │      Min │      Max │
├─────────────────────┼────────────────┼───────┼──────────┼──────────┤
│          layer_perm │ 1.97e-13 ± 0.0 │     3 │ 9.87e-15 │ 1.48e-12 │
│ layer_heat_capacity │ 400.0 ± 0.0    │     3 │    400.0 │   1000.0 │
│    layer_porosities │ 0.2 ± 2.78e-17 │     3 │     0.05 │     0.35 │
└─────────────────────┴────────────────┴───────┴──────────┴──────────┘
Inactive optimization parameters
┌─────────────────────────┬──────────────────┬───────┬─────┬─────┐
│                    Name │ Initial value    │ Count │ Min │ Max │
├─────────────────────────┼──────────────────┼───────┼─────┼─────┤
│          injection_rate │ 0.015 ± 3.47e-18 │    10 │   - │   - │
│ injection_temperature_C │ 15.0 ± 0.0       │    10 │   - │   - │
└─────────────────────────┴──────────────────┴───────┴─────┴─────┘
No multipliers set.

Call the optimizer

Now that we have freed a few parameters, we can call the optimizer with the objective function. The defaults for the optimizer are fairly reasonable, so we do not tweak the convergence criteria or the maximum number of iterations. Note that by default the optimizer uses LBFGS, but it is also possible to pass other optimizers as a function callable. The default for the optimizer is to minimize the objective function, which is the case for a history match. By passing for example lbfgs_num = 1, max_it = 50 it is possible to obtain a better match, but this is not necessary for the purpose of this example.

prm_opt = JutulDarcy.optimize_reservoir(opt, mismatch_objective, max_it = 50, gradient_scaling = false, optimizer = :lbfgsb_qp);

setup_reservoir_state: Received primary variable Saturations, but this is not known to reservoir model.
Optimization: Starting calibration of 9 parameters.
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Setting up adjoint storage.
Optimization: Finished setup in 68.221241894 seconds.
Optimization: Adjoint solve took 38.643207385 seconds.

Optimization: Objective #1: 1.81499e+01, gradient 2-norm: 8.40785e+12
It:  0 | v: 1.815e+01 | ls-its:  0 | pg: 8.03e+12 | ρ:       NaN | qp-its:  0 +  0 | n-active:   0
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.873170902 seconds.

Optimization: Objective #2: 5.85646e+01 (f/f0=3.227e+00), gradient 2-norm: 5.74716e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.942065452 seconds.

Optimization: Objective #3: 1.42655e+01 (f/f0=7.860e-01), gradient 2-norm: 3.55326e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.923991368 seconds.

Optimization: Objective #4: 5.85646e+01 (f/f0=3.227e+00), gradient 2-norm: 5.74716e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.932651087 seconds.

Optimization: Objective #5: 1.56059e+01 (f/f0=8.598e-01), gradient 2-norm: 2.68161e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.881535735 seconds.

Optimization: Objective #6: 1.36118e+01 (f/f0=7.500e-01), gradient 2-norm: 5.83781e+13
Hessian not updated during iteration 1.
It:  1 | v: 1.361e+01 | ls-its:  5 | pg: 5.18e+13 | ρ:  1.35e+00 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.826084321 seconds.

Optimization: Objective #7: 1.84651e+01 (f/f0=1.017e+00), gradient 2-norm: 2.51501e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.939973477 seconds.

Optimization: Objective #8: 2.01529e+01 (f/f0=1.110e+00), gradient 2-norm: 3.14677e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.848207929 seconds.

Optimization: Objective #9: 1.56340e+01 (f/f0=8.614e-01), gradient 2-norm: 5.51693e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.951107396 seconds.

Optimization: Objective #10: 1.34540e+01 (f/f0=7.413e-01), gradient 2-norm: 4.57268e+13
Hessian not updated during iteration 2.
It:  2 | v: 1.345e+01 | ls-its:  4 | pg: 4.06e+13 | ρ:  1.40e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.907482057 seconds.

Optimization: Objective #11: 6.27248e+01 (f/f0=3.456e+00), gradient 2-norm: 6.13877e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.905738203 seconds.

Optimization: Objective #12: 1.26267e+01 (f/f0=6.957e-01), gradient 2-norm: 3.21132e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.918492637 seconds.

Optimization: Objective #13: 1.13807e+01 (f/f0=6.270e-01), gradient 2-norm: 1.14628e+14
Hessian not updated during iteration 3.
It:  3 | v: 1.138e+01 | ls-its:  3 | pg: 1.08e+14 | ρ:  7.99e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.797206271 seconds.

Optimization: Objective #14: 1.76893e+01 (f/f0=9.746e-01), gradient 2-norm: 2.34045e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.847806756 seconds.

Optimization: Objective #15: 1.86313e+01 (f/f0=1.027e+00), gradient 2-norm: 4.05026e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.849753125 seconds.

Optimization: Objective #16: 1.38003e+01 (f/f0=7.604e-01), gradient 2-norm: 6.70483e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.955567417 seconds.

Optimization: Objective #17: 1.07225e+01 (f/f0=5.908e-01), gradient 2-norm: 7.08001e+13
Hessian not updated during iteration 4.
It:  4 | v: 1.072e+01 | ls-its:  4 | pg: 6.38e+13 | ρ:  1.88e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.917853851 seconds.

Optimization: Objective #18: 6.33532e+01 (f/f0=3.491e+00), gradient 2-norm: 6.17373e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.884639925 seconds.

Optimization: Objective #19: 1.08161e+01 (f/f0=5.959e-01), gradient 2-norm: 3.33160e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.950835089 seconds.

Optimization: Objective #20: 8.76220e+00 (f/f0=4.828e-01), gradient 2-norm: 9.97974e+13
Hessian not updated during iteration 5.
It:  5 | v: 8.762e+00 | ls-its:  3 | pg: 8.30e+13 | ρ:  7.36e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.856944422 seconds.

Optimization: Objective #21: 1.67969e+01 (f/f0=9.255e-01), gradient 2-norm: 1.92142e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.898210684 seconds.

Optimization: Objective #22: 1.70529e+01 (f/f0=9.396e-01), gradient 2-norm: 4.78261e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.880122964 seconds.

Optimization: Objective #23: 1.15286e+01 (f/f0=6.352e-01), gradient 2-norm: 8.12134e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.930430432 seconds.

Optimization: Objective #24: 8.41309e+00 (f/f0=4.635e-01), gradient 2-norm: 8.49765e+13
Hessian not updated during iteration 6.
It:  6 | v: 8.413e+00 | ls-its:  4 | pg: 7.98e+13 | ρ:  1.75e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.942655594 seconds.

Optimization: Objective #25: 6.40248e+01 (f/f0=3.528e+00), gradient 2-norm: 6.20940e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.867240038 seconds.

Optimization: Objective #26: 1.05522e+01 (f/f0=5.814e-01), gradient 2-norm: 3.86686e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 3.497909121 seconds.

Optimization: Objective #27: 7.18648e+00 (f/f0=3.960e-01), gradient 2-norm: 9.47106e+13
Hessian not updated during iteration 7.
It:  7 | v: 7.186e+00 | ls-its:  3 | pg: 6.97e+13 | ρ:  6.66e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.870611587 seconds.

Optimization: Objective #28: 1.63057e+01 (f/f0=8.984e-01), gradient 2-norm: 1.44108e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.918461893 seconds.

Optimization: Objective #29: 1.58417e+01 (f/f0=8.728e-01), gradient 2-norm: 5.18004e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.985881633 seconds.

Optimization: Objective #30: 1.00076e+01 (f/f0=5.514e-01), gradient 2-norm: 8.97529e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.93455264 seconds.

Optimization: Objective #31: 6.97730e+00 (f/f0=3.844e-01), gradient 2-norm: 9.21663e+13
Hessian not updated during iteration 8.
It:  8 | v: 6.977e+00 | ls-its:  4 | pg: 8.81e+13 | ρ:  1.57e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.933782613 seconds.

Optimization: Objective #32: 6.44678e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23182e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.844239055 seconds.

Optimization: Objective #33: 1.05931e+01 (f/f0=5.836e-01), gradient 2-norm: 4.19768e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.974739753 seconds.

Optimization: Objective #34: 6.17543e+00 (f/f0=3.402e-01), gradient 2-norm: 8.78918e+13
Hessian not updated during iteration 9.
It:  9 | v: 6.175e+00 | ls-its:  3 | pg: 7.01e+13 | ρ:  6.49e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.888735284 seconds.

Optimization: Objective #35: 1.62273e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31302e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 1.035130899 seconds.

Optimization: Objective #36: 1.50089e+01 (f/f0=8.269e-01), gradient 2-norm: 5.37728e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.855939221 seconds.

Optimization: Objective #37: 8.65614e+00 (f/f0=4.769e-01), gradient 2-norm: 9.69542e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.880303171 seconds.

Optimization: Objective #38: 6.05543e+00 (f/f0=3.336e-01), gradient 2-norm: 9.31091e+13
Hessian not updated during iteration 10.
It: 10 | v: 6.055e+00 | ls-its:  4 | pg: 9.06e+13 | ρ:  1.63e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.914596574 seconds.

Optimization: Objective #39: 6.44696e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23201e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.896249571 seconds.

Optimization: Objective #40: 1.08660e+01 (f/f0=5.987e-01), gradient 2-norm: 4.44329e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.820607698 seconds.

Optimization: Objective #41: 5.60421e+00 (f/f0=3.088e-01), gradient 2-norm: 8.26109e+13
Hessian not updated during iteration 11.
It: 11 | v: 5.604e+00 | ls-its:  3 | pg: 7.55e+13 | ρ:  6.45e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.842918594 seconds.

Optimization: Objective #42: 1.62273e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31272e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.97117977 seconds.

Optimization: Objective #43: 1.43325e+01 (f/f0=7.897e-01), gradient 2-norm: 5.62771e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.807148763 seconds.

Optimization: Objective #44: 7.16109e+00 (f/f0=3.946e-01), gradient 2-norm: 1.03940e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.930817983 seconds.

Optimization: Objective #45: 5.52793e+00 (f/f0=3.046e-01), gradient 2-norm: 8.97159e+13
Hessian not updated during iteration 12.
It: 12 | v: 5.528e+00 | ls-its:  4 | pg: 8.90e+13 | ρ:  2.74e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.912665052 seconds.

Optimization: Objective #46: 6.44703e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23208e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.914821423 seconds.

Optimization: Objective #47: 1.12814e+01 (f/f0=6.216e-01), gradient 2-norm: 4.69052e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.889090239 seconds.

Optimization: Objective #48: 5.32345e+00 (f/f0=2.933e-01), gradient 2-norm: 8.16699e+13
Hessian not updated during iteration 13.
It: 13 | v: 5.323e+00 | ls-its:  3 | pg: 7.73e+13 | ρ:  6.40e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.916960369 seconds.

Optimization: Objective #49: 1.62273e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31258e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.869119979 seconds.

Optimization: Objective #50: 1.38945e+01 (f/f0=7.655e-01), gradient 2-norm: 5.79281e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.883224585 seconds.

Optimization: Objective #51: 6.42360e+00 (f/f0=3.539e-01), gradient 2-norm: 1.05416e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.88434689 seconds.

Optimization: Objective #52: 5.26907e+00 (f/f0=2.903e-01), gradient 2-norm: 8.76928e+13
Hessian not updated during iteration 14.
It: 14 | v: 5.269e+00 | ls-its:  4 | pg: 8.74e+13 | ρ:  3.32e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.77633624 seconds.

Optimization: Objective #53: 6.44707e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23213e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.855948337 seconds.

Optimization: Objective #54: 1.14159e+01 (f/f0=6.290e-01), gradient 2-norm: 4.77424e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.767857351 seconds.

Optimization: Objective #55: 5.13834e+00 (f/f0=2.831e-01), gradient 2-norm: 8.07871e+13
Hessian not updated during iteration 15.
It: 15 | v: 5.138e+00 | ls-its:  3 | pg: 7.77e+13 | ρ:  6.47e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.805492169 seconds.

Optimization: Objective #56: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31250e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.759586176 seconds.

Optimization: Objective #57: 1.35549e+01 (f/f0=7.468e-01), gradient 2-norm: 5.91906e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.764145866 seconds.

Optimization: Objective #58: 5.96626e+00 (f/f0=3.287e-01), gradient 2-norm: 1.05188e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.85163036 seconds.

Optimization: Objective #59: 5.09648e+00 (f/f0=2.808e-01), gradient 2-norm: 8.64863e+13
Hessian not updated during iteration 16.
It: 16 | v: 5.096e+00 | ls-its:  4 | pg: 8.63e+13 | ρ:  3.68e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.785828129 seconds.

Optimization: Objective #60: 6.44711e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23216e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.861372719 seconds.

Optimization: Objective #61: 1.14831e+01 (f/f0=6.327e-01), gradient 2-norm: 4.81709e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.766117776 seconds.

Optimization: Objective #62: 5.00206e+00 (f/f0=2.756e-01), gradient 2-norm: 8.00322e+13
Hessian not updated during iteration 17.
It: 17 | v: 5.002e+00 | ls-its:  3 | pg: 7.76e+13 | ρ:  6.48e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.897702134 seconds.

Optimization: Objective #63: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31244e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.760657688 seconds.

Optimization: Objective #64: 1.32664e+01 (f/f0=7.309e-01), gradient 2-norm: 6.02746e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.774869147 seconds.

Optimization: Objective #65: 5.64382e+00 (f/f0=3.110e-01), gradient 2-norm: 1.04153e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.831936182 seconds.

Optimization: Objective #66: 4.96850e+00 (f/f0=2.737e-01), gradient 2-norm: 8.52709e+13
Hessian not updated during iteration 18.
It: 18 | v: 4.968e+00 | ls-its:  4 | pg: 8.52e+13 | ρ:  3.93e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.879719178 seconds.

Optimization: Objective #67: 6.44714e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23219e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.952517467 seconds.

Optimization: Objective #68: 1.15256e+01 (f/f0=6.350e-01), gradient 2-norm: 4.84408e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.843949715 seconds.

Optimization: Objective #69: 4.89578e+00 (f/f0=2.697e-01), gradient 2-norm: 7.93446e+13
Hessian not updated during iteration 19.
It: 19 | v: 4.896e+00 | ls-its:  3 | pg: 7.74e+13 | ρ:  6.52e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.88981785 seconds.

Optimization: Objective #70: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31239e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 1.016270177 seconds.

Optimization: Objective #71: 1.30132e+01 (f/f0=7.170e-01), gradient 2-norm: 6.12277e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.878661005 seconds.

Optimization: Objective #72: 5.40522e+00 (f/f0=2.978e-01), gradient 2-norm: 1.02758e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.839027371 seconds.

Optimization: Objective #73: 4.86813e+00 (f/f0=2.682e-01), gradient 2-norm: 8.42347e+13
Hessian not updated during iteration 20.
It: 20 | v: 4.868e+00 | ls-its:  4 | pg: 8.42e+13 | ρ:  4.10e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.826774289 seconds.

Optimization: Objective #74: 6.44717e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23221e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.857688389 seconds.

Optimization: Objective #75: 1.15544e+01 (f/f0=6.366e-01), gradient 2-norm: 4.86224e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.938752491 seconds.

Optimization: Objective #76: 4.80966e+00 (f/f0=2.650e-01), gradient 2-norm: 7.86708e+13
Hessian not updated during iteration 21.
It: 21 | v: 4.810e+00 | ls-its:  3 | pg: 7.70e+13 | ρ:  6.55e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.813639253 seconds.

Optimization: Objective #77: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31235e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.836752635 seconds.

Optimization: Objective #78: 1.27847e+01 (f/f0=7.044e-01), gradient 2-norm: 6.20814e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.787227343 seconds.

Optimization: Objective #79: 5.22083e+00 (f/f0=2.877e-01), gradient 2-norm: 1.01258e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.817427703 seconds.

Optimization: Objective #80: 4.78637e+00 (f/f0=2.637e-01), gradient 2-norm: 8.32492e+13
Hessian not updated during iteration 22.
It: 22 | v: 4.786e+00 | ls-its:  4 | pg: 8.32e+13 | ρ:  4.24e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.93040985 seconds.

Optimization: Objective #81: 6.44719e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23224e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.858687838 seconds.

Optimization: Objective #82: 1.15758e+01 (f/f0=6.378e-01), gradient 2-norm: 4.87560e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.966110203 seconds.

Optimization: Objective #83: 4.73802e+00 (f/f0=2.610e-01), gradient 2-norm: 7.80118e+13
Hessian not updated during iteration 23.
It: 23 | v: 4.738e+00 | ls-its:  3 | pg: 7.66e+13 | ρ:  6.58e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.785458584 seconds.

Optimization: Objective #84: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31231e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.759891007 seconds.

Optimization: Objective #85: 1.25751e+01 (f/f0=6.928e-01), gradient 2-norm: 6.28747e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.78492594 seconds.

Optimization: Objective #86: 5.07420e+00 (f/f0=2.796e-01), gradient 2-norm: 9.96629e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.762496929 seconds.

Optimization: Objective #87: 4.71810e+00 (f/f0=2.600e-01), gradient 2-norm: 8.23425e+13
Hessian not updated during iteration 24.
It: 24 | v: 4.718e+00 | ls-its:  4 | pg: 8.23e+13 | ρ:  4.34e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.924342299 seconds.

Optimization: Objective #88: 6.44721e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23226e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.780540274 seconds.

Optimization: Objective #89: 1.15922e+01 (f/f0=6.387e-01), gradient 2-norm: 4.88565e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.853345725 seconds.

Optimization: Objective #90: 4.67720e+00 (f/f0=2.577e-01), gradient 2-norm: 7.73701e+13
Hessian not updated during iteration 25.
It: 25 | v: 4.677e+00 | ls-its:  3 | pg: 7.61e+13 | ρ:  6.60e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.822766538 seconds.

Optimization: Objective #91: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31228e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.880840162 seconds.

Optimization: Objective #92: 1.23797e+01 (f/f0=6.821e-01), gradient 2-norm: 6.36370e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.817933792 seconds.

Optimization: Objective #93: 4.95467e+00 (f/f0=2.730e-01), gradient 2-norm: 9.80300e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.765260773 seconds.

Optimization: Objective #94: 4.65990e+00 (f/f0=2.567e-01), gradient 2-norm: 8.14944e+13
Hessian not updated during iteration 26.
It: 26 | v: 4.660e+00 | ls-its:  4 | pg: 8.15e+13 | ρ:  4.43e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.852094183 seconds.

Optimization: Objective #95: 6.44723e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23228e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.77451497 seconds.

Optimization: Objective #96: 1.16057e+01 (f/f0=6.394e-01), gradient 2-norm: 4.89367e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.905862713 seconds.

Optimization: Objective #97: 4.62477e+00 (f/f0=2.548e-01), gradient 2-norm: 7.67684e+13
Hessian not updated during iteration 27.
It: 27 | v: 4.625e+00 | ls-its:  3 | pg: 7.57e+13 | ρ:  6.62e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.7687348 seconds.

Optimization: Objective #98: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31225e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.942059138 seconds.

Optimization: Objective #99: 1.21973e+01 (f/f0=6.720e-01), gradient 2-norm: 6.43374e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.846747362 seconds.

Optimization: Objective #100: 4.85621e+00 (f/f0=2.676e-01), gradient 2-norm: 9.64619e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.933288114 seconds.

Optimization: Objective #101: 4.60960e+00 (f/f0=2.540e-01), gradient 2-norm: 8.06822e+13
Hessian not updated during iteration 28.
It: 28 | v: 4.610e+00 | ls-its:  4 | pg: 8.07e+13 | ρ:  4.50e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.949376832 seconds.

Optimization: Objective #102: 6.44725e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23230e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.816960142 seconds.

Optimization: Objective #103: 1.16167e+01 (f/f0=6.400e-01), gradient 2-norm: 4.90009e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.864666936 seconds.

Optimization: Objective #104: 4.57900e+00 (f/f0=2.523e-01), gradient 2-norm: 7.61850e+13
Hessian not updated during iteration 29.
It: 29 | v: 4.579e+00 | ls-its:  3 | pg: 7.52e+13 | ρ:  6.63e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.766946496 seconds.

Optimization: Objective #105: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31223e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 1.049406662 seconds.

Optimization: Objective #106: 1.20246e+01 (f/f0=6.625e-01), gradient 2-norm: 6.50042e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.771016774 seconds.

Optimization: Objective #107: 4.77336e+00 (f/f0=2.630e-01), gradient 2-norm: 9.49106e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 3.128573427 seconds.

Optimization: Objective #108: 4.56558e+00 (f/f0=2.515e-01), gradient 2-norm: 7.99270e+13
Hessian not updated during iteration 30.
It: 30 | v: 4.566e+00 | ls-its:  4 | pg: 7.99e+13 | ρ:  4.55e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.809350193 seconds.

Optimization: Objective #109: 6.44726e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23232e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.888930893 seconds.

Optimization: Objective #110: 1.16262e+01 (f/f0=6.406e-01), gradient 2-norm: 4.90535e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.891601436 seconds.

Optimization: Objective #111: 4.53863e+00 (f/f0=2.501e-01), gradient 2-norm: 7.56011e+13
Hessian not updated during iteration 31.
It: 31 | v: 4.539e+00 | ls-its:  3 | pg: 7.47e+13 | ρ:  6.65e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.862305323 seconds.

Optimization: Objective #112: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31221e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.804900541 seconds.

Optimization: Objective #113: 1.18623e+01 (f/f0=6.536e-01), gradient 2-norm: 6.56092e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.943616229 seconds.

Optimization: Objective #114: 4.70344e+00 (f/f0=2.591e-01), gradient 2-norm: 9.34183e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 1.066254529 seconds.

Optimization: Objective #115: 4.52666e+00 (f/f0=2.494e-01), gradient 2-norm: 7.91913e+13
Hessian not updated during iteration 32.
It: 32 | v: 4.527e+00 | ls-its:  4 | pg: 7.92e+13 | ρ:  4.60e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.857246901 seconds.

Optimization: Objective #116: 6.44740e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23242e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.889518959 seconds.

Optimization: Objective #117: 1.16343e+01 (f/f0=6.410e-01), gradient 2-norm: 4.90968e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.837020233 seconds.

Optimization: Objective #118: 4.50271e+00 (f/f0=2.481e-01), gradient 2-norm: 7.50541e+13
Hessian not updated during iteration 33.
It: 33 | v: 4.503e+00 | ls-its:  3 | pg: 7.43e+13 | ρ:  6.66e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.850583287 seconds.

Optimization: Objective #119: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31219e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.878540418 seconds.

Optimization: Objective #120: 1.17059e+01 (f/f0=6.450e-01), gradient 2-norm: 6.62420e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.916959544 seconds.

Optimization: Objective #121: 4.64288e+00 (f/f0=2.558e-01), gradient 2-norm: 9.20085e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.832536196 seconds.

Optimization: Objective #122: 4.49196e+00 (f/f0=2.475e-01), gradient 2-norm: 7.84896e+13
Hessian not updated during iteration 34.
It: 34 | v: 4.492e+00 | ls-its:  4 | pg: 7.85e+13 | ρ:  4.64e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.922297732 seconds.

Optimization: Objective #123: 6.44729e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23235e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.85327852 seconds.

Optimization: Objective #124: 1.16417e+01 (f/f0=6.414e-01), gradient 2-norm: 4.91353e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.797348321 seconds.

Optimization: Objective #125: 4.47053e+00 (f/f0=2.463e-01), gradient 2-norm: 7.45046e+13
Hessian not updated during iteration 35.
It: 35 | v: 4.471e+00 | ls-its:  3 | pg: 7.38e+13 | ρ:  6.66e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.904326314 seconds.

Optimization: Objective #126: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31218e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.840606693 seconds.

Optimization: Objective #127: 1.15592e+01 (f/f0=6.369e-01), gradient 2-norm: 6.68297e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.937149752 seconds.

Optimization: Objective #128: 4.59095e+00 (f/f0=2.529e-01), gradient 2-norm: 9.06549e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.843145942 seconds.

Optimization: Objective #129: 4.46081e+00 (f/f0=2.458e-01), gradient 2-norm: 7.78244e+13
Hessian not updated during iteration 36.
It: 36 | v: 4.461e+00 | ls-its:  4 | pg: 7.78e+13 | ρ:  4.67e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.979264816 seconds.

Optimization: Objective #130: 6.44730e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23236e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.878378181 seconds.

Optimization: Objective #131: 1.16480e+01 (f/f0=6.418e-01), gradient 2-norm: 4.91672e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.932649886 seconds.

Optimization: Objective #132: 4.44147e+00 (f/f0=2.447e-01), gradient 2-norm: 7.40047e+13
Hessian not updated during iteration 37.
It: 37 | v: 4.441e+00 | ls-its:  3 | pg: 7.34e+13 | ρ:  6.68e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.946221235 seconds.

Optimization: Objective #133: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31216e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.865630354 seconds.

Optimization: Objective #134: 1.14149e+01 (f/f0=6.289e-01), gradient 2-norm: 6.73833e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.970642592 seconds.

Optimization: Objective #135: 4.54490e+00 (f/f0=2.504e-01), gradient 2-norm: 8.93425e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.866433763 seconds.

Optimization: Objective #136: 4.43265e+00 (f/f0=2.442e-01), gradient 2-norm: 7.72119e+13
Hessian not updated during iteration 38.
It: 38 | v: 4.433e+00 | ls-its:  4 | pg: 7.72e+13 | ρ:  4.70e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.9658936 seconds.

Optimization: Objective #137: 6.44732e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23238e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.863768376 seconds.

Optimization: Objective #138: 1.16538e+01 (f/f0=6.421e-01), gradient 2-norm: 4.91959e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.849752456 seconds.

Optimization: Objective #139: 4.41511e+00 (f/f0=2.433e-01), gradient 2-norm: 7.35067e+13
Hessian not updated during iteration 39.
It: 39 | v: 4.415e+00 | ls-its:  3 | pg: 7.29e+13 | ρ:  6.68e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.805140833 seconds.

Optimization: Objective #140: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31214e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.764783497 seconds.

Optimization: Objective #141: 1.12792e+01 (f/f0=6.214e-01), gradient 2-norm: 6.79141e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.895650846 seconds.

Optimization: Objective #142: 4.50478e+00 (f/f0=2.482e-01), gradient 2-norm: 8.81339e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.839285644 seconds.

Optimization: Objective #143: 4.40706e+00 (f/f0=2.428e-01), gradient 2-norm: 7.66035e+13
Hessian not updated during iteration 40.
It: 40 | v: 4.407e+00 | ls-its:  4 | pg: 7.66e+13 | ρ:  4.72e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.90363492 seconds.

Optimization: Objective #144: 6.44733e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23239e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.879289529 seconds.

Optimization: Objective #145: 1.16592e+01 (f/f0=6.424e-01), gradient 2-norm: 4.92214e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.85079172 seconds.

Optimization: Objective #146: 4.39107e+00 (f/f0=2.419e-01), gradient 2-norm: 7.30034e+13
Hessian not updated during iteration 41.
It: 41 | v: 4.391e+00 | ls-its:  3 | pg: 7.25e+13 | ρ:  6.68e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.850537249 seconds.

Optimization: Objective #147: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31213e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.824339855 seconds.

Optimization: Objective #148: 1.11496e+01 (f/f0=6.143e-01), gradient 2-norm: 6.84080e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 3.22373527 seconds.

Optimization: Objective #149: 4.46927e+00 (f/f0=2.462e-01), gradient 2-norm: 8.69924e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.877442433 seconds.

Optimization: Objective #150: 4.38367e+00 (f/f0=2.415e-01), gradient 2-norm: 7.60032e+13
Hessian not updated during iteration 42.
It: 42 | v: 4.384e+00 | ls-its:  4 | pg: 7.60e+13 | ρ:  4.75e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.940055921 seconds.

Optimization: Objective #151: 6.44734e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23240e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.882685927 seconds.

Optimization: Objective #152: 1.16640e+01 (f/f0=6.426e-01), gradient 2-norm: 4.92437e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.915365873 seconds.

Optimization: Objective #153: 4.36903e+00 (f/f0=2.407e-01), gradient 2-norm: 7.25378e+13
Hessian not updated during iteration 43.
It: 43 | v: 4.369e+00 | ls-its:  3 | pg: 7.20e+13 | ρ:  6.69e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 1.19249162 seconds.

Optimization: Objective #154: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31211e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.893569565 seconds.

Optimization: Objective #155: 1.10228e+01 (f/f0=6.073e-01), gradient 2-norm: 6.89201e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.936917272 seconds.

Optimization: Objective #156: 4.43730e+00 (f/f0=2.445e-01), gradient 2-norm: 8.58692e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 1.050009362 seconds.

Optimization: Objective #157: 4.36223e+00 (f/f0=2.403e-01), gradient 2-norm: 7.54447e+13
Hessian not updated during iteration 44.
It: 44 | v: 4.362e+00 | ls-its:  4 | pg: 7.54e+13 | ρ:  4.76e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.913900148 seconds.

Optimization: Objective #158: 6.44735e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23241e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.923973218 seconds.

Optimization: Objective #159: 1.16684e+01 (f/f0=6.429e-01), gradient 2-norm: 4.92644e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.888882531 seconds.

Optimization: Objective #160: 4.34875e+00 (f/f0=2.396e-01), gradient 2-norm: 7.20904e+13
Hessian not updated during iteration 45.
It: 45 | v: 4.349e+00 | ls-its:  3 | pg: 7.16e+13 | ρ:  6.69e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 1.041369538 seconds.

Optimization: Objective #161: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31210e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.90158818 seconds.

Optimization: Objective #162: 1.09007e+01 (f/f0=6.006e-01), gradient 2-norm: 6.94315e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 1.062606647 seconds.

Optimization: Objective #163: 4.40864e+00 (f/f0=2.429e-01), gradient 2-norm: 8.48133e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.898822095 seconds.

Optimization: Objective #164: 4.34248e+00 (f/f0=2.393e-01), gradient 2-norm: 7.48987e+13
Hessian not updated during iteration 46.
It: 46 | v: 4.342e+00 | ls-its:  4 | pg: 7.49e+13 | ρ:  4.78e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.943188565 seconds.

Optimization: Objective #165: 6.44736e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23241e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.877573423 seconds.

Optimization: Objective #166: 1.16727e+01 (f/f0=6.431e-01), gradient 2-norm: 4.92831e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.835483623 seconds.

Optimization: Objective #167: 4.33005e+00 (f/f0=2.386e-01), gradient 2-norm: 7.16558e+13
Hessian not updated during iteration 47.
It: 47 | v: 4.330e+00 | ls-its:  3 | pg: 7.12e+13 | ρ:  6.70e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.867836832 seconds.

Optimization: Objective #168: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31209e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.815456722 seconds.

Optimization: Objective #169: 1.07818e+01 (f/f0=5.940e-01), gradient 2-norm: 6.99199e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 1.021615346 seconds.

Optimization: Objective #170: 4.38271e+00 (f/f0=2.415e-01), gradient 2-norm: 8.38040e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.884463386 seconds.

Optimization: Objective #171: 4.32423e+00 (f/f0=2.383e-01), gradient 2-norm: 7.44021e+13
Hessian not updated during iteration 48.
It: 48 | v: 4.324e+00 | ls-its:  4 | pg: 7.44e+13 | ρ:  4.81e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.921637657 seconds.

Optimization: Objective #172: 6.44737e+01 (f/f0=3.552e+00), gradient 2-norm: 6.23243e+15
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.913140008 seconds.

Optimization: Objective #173: 1.16766e+01 (f/f0=6.433e-01), gradient 2-norm: 4.93001e+14
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.915054564 seconds.

Optimization: Objective #174: 4.31272e+00 (f/f0=2.376e-01), gradient 2-norm: 7.12238e+13
Hessian not updated during iteration 49.
It: 49 | v: 4.313e+00 | ls-its:  3 | pg: 7.08e+13 | ρ:  6.70e-01 | qp-its:  1 +  0 | n-active:   3
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.936515163 seconds.

Optimization: Objective #175: 1.62274e+01 (f/f0=8.941e-01), gradient 2-norm: 1.31208e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.899816576 seconds.

Optimization: Objective #176: 1.06686e+01 (f/f0=5.878e-01), gradient 2-norm: 7.03663e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.993644714 seconds.

Optimization: Objective #177: 4.35932e+00 (f/f0=2.402e-01), gradient 2-norm: 8.28852e+13
Jutul: Simulating 30 years, 11.82 weeks as 92 report steps
Optimization: Adjoint solve took 0.885010686 seconds.

Optimization: Objective #178: 4.30732e+00 (f/f0=2.373e-01), gradient 2-norm: 7.38933e+13
Hessian not updated during iteration 50.
It: 50 | v: 4.307e+00 | ls-its:  4 | pg: 7.39e+13 | ρ:  4.81e-01 | qp-its:  1 +  0 | n-active:   3
Optimization: Finished in 451.543866352 seconds.

Print the optimization overview

If we display the optimization overview, we can see that there are now additional columns indicating the optimized values. Note that while the permeability and porosities are well matched, the heat capacity of the low permeable layers are not very accurate. There is likely not enough data in the production profiles to constrain the heat capacity of the low permeable layers, as there is limited heat siphoned from these layers in the truth case.

opt

DictParameters with 5 parameters (3 active), and 0 multipliers:
Active optimization parameters
┌─────────────────────┬────────────────┬───────┬──────────┬──────────┬──────────
│                Name │ Initial value  │ Count │      Min │      Max │ Optimiz ⋯
├─────────────────────┼────────────────┼───────┼──────────┼──────────┼──────────
│          layer_perm │ 1.97e-13 ± 0.0 │     3 │ 9.87e-15 │ 1.48e-12 │ 1.45e-1 ⋯
│ layer_heat_capacity │ 400.0 ± 0.0    │     3 │    400.0 │   1000.0 │ 400.0 ± ⋯
│    layer_porosities │ 0.2 ± 2.78e-17 │     3 │     0.05 │     0.35 │ 0.0621, ⋯
└─────────────────────┴────────────────┴───────┴──────────┴──────────┴──────────
                                                               2 columns omitted
Inactive optimization parameters
┌─────────────────────────┬──────────────────┬───────┬─────┬─────┐
│                    Name │ Initial value    │ Count │ Min │ Max │
├─────────────────────────┼──────────────────┼───────┼─────┼─────┤
│          injection_rate │ 0.015 ± 3.47e-18 │    10 │   - │   - │
│ injection_temperature_C │ 15.0 ± 0.0       │    10 │   - │   - │
└─────────────────────────┴──────────────────┴───────┴─────┴─────┘
No multipliers set.

Simulate the optimized case

case_opt = setup_doublet_case(prm_opt)
ws_opt, states_opt = simulate_reservoir(case_opt)

ReservoirSimResult with 92 entries:

  wells (2 present):
    :Producer
    :Injector
    Results per well:
       :lrat => Vector{Float64} of size (92,)
       :wrat => Vector{Float64} of size (92,)
       :temperature => Vector{Float64} of size (92,)
       :control => Vector{Symbol} of size (92,)
       :Aqueous_mass_rate => Vector{Float64} of size (92,)
       :bhp => Vector{Float64} of size (92,)
       :wcut => Vector{Float64} of size (92,)
       :mass_rate => Vector{Float64} of size (92,)
       :rate => Vector{Float64} of size (92,)
       :mrat => Vector{Float64} of size (92,)

  states (Vector with 92 entries, reservoir variables for each state)
    :Pressure => Vector{Float64} of size (1000,)
    :TotalMasses => Matrix{Float64} of size (1, 1000)
    :TotalThermalEnergy => Vector{Float64} of size (1000,)
    :FluidEnthalpy => Matrix{Float64} of size (1, 1000)
    :Temperature => Vector{Float64} of size (1000,)
    :PhaseMassDensities => Matrix{Float64} of size (1, 1000)
    :RockInternalEnergy => Vector{Float64} of size (1000,)
    :FluidInternalEnergy => Matrix{Float64} of size (1, 1000)

  time (report time for each state)
     Vector{Float64} of length 92

  result (extended states, reports)
     SimResult with 92 entries

  extra
     Dict{Any, Any} with keys :simulator, :config

  Completed at Mar. 10 2026 09:10 after 1 second, 33 milliseconds, 263.1 microseconds.

Plot the well responses

We plot the well responses for the producer temperature, producer water rate, and injector bottom hole pressure. These values represent the data used in the objective function. We observe good match, which is consistent with the reduction in the objective function valeu during the optimization.

get_wtime(w) = convert_from_si.(w.time, :day)
get_prod_temp(w) = convert_from_si.(w[:Producer, :temperature], :Celsius)
get_prod_rate(w) = -w[:Producer, :wrat]/si_unit(:liter)
get_inj_bhp(w) = convert_from_si.(w[:Injector, :bhp], :bar)

fig = Figure(size = (1200, 800))
ax = Axis(fig[1, 1], title = "Producer temperature", ylabel = "Temperature (°C)", xlabel = "Time (days)")
scatter!(ax, get_wtime(ws), get_prod_temp(ws), label = "Truth")
lines!(ax, get_wtime(ws_guess), get_prod_temp(ws_guess), label = "Initial guess")
lines!(ax, get_wtime(ws_opt), get_prod_temp(ws_opt), label = "Optimized")
axislegend(position = :rc)
ax = Axis(fig[2, 1], title = "Producer water rate", ylabel = "Liter / s", xlabel = "Time (days)")
scatter!(ax, get_wtime(ws), get_prod_rate(ws), label = "Truth")
lines!(ax, get_wtime(ws_guess), get_prod_rate(ws_guess), label = "Initial guess")
lines!(ax, get_wtime(ws_opt), get_prod_rate(ws_opt), label = "Optimized")
axislegend(position = :rc)
ax = Axis(fig[3, 1], title = "Producer bottom hole pressure", ylabel = "Pressure (bar)", xlabel = "Time (days)")
scatter!(ax, get_wtime(ws), get_inj_bhp(ws), label = "Truth")
lines!(ax, get_wtime(ws_guess), get_inj_bhp(ws_guess), label = "Initial guess")
lines!(ax, get_wtime(ws_opt), get_inj_bhp(ws_opt), label = "Optimized")
axislegend(position = :rc)
fig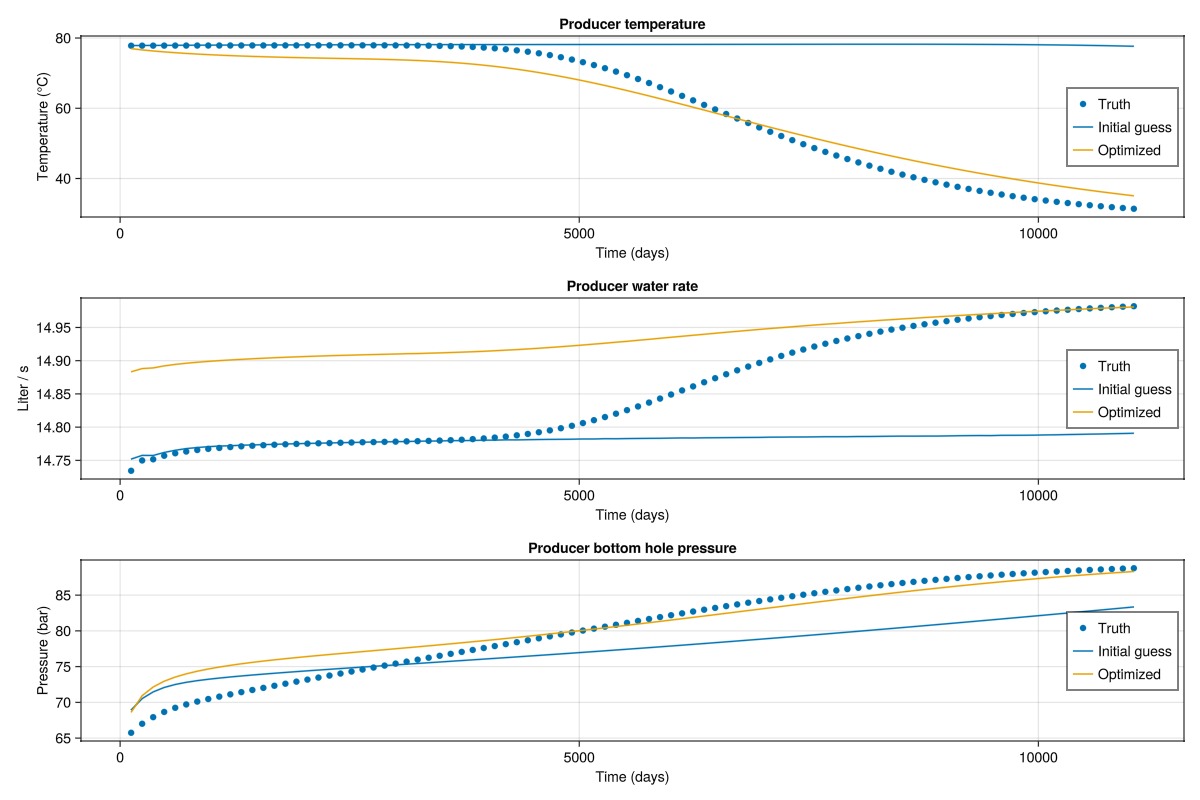

Plot the spatial results

We plot the spatial results for the truth case, the initial guess, and the optimized case. The temperature is plotted in Celsius and we use the same color scale for all steps. Note that in terms of the optimizer itself, this is hidden data: The objective function only matches the well responses. Getting a good match in the spatial distribution of temperature is a side-effect of the physics and parametrization of the model, as different physics or a different parameterization could lead to good match in terms of the objective function, even without good match for the spatial distribution.

step = 80
cmap = reverse(to_colormap(:heat))
fig = Figure(size = (1200, 400))
ax = Axis3(fig[1, 1], title = "Truth")
plot_cell_data!(ax, rmesh, states[step][:Temperature] .- 273.15, colorrange = (10.0, 100.0), colormap = cmap)
ax.elevation[] = 0.0
ax.azimuth[] = -π/2
hidedecorations!(ax)

ax = Axis3(fig[1, 2], title = "Initial guess")
plot_cell_data!(ax, rmesh, states_guess[step][:Temperature] .- 273.15, colorrange = (10.0, 100.0), colormap = cmap)
ax.elevation[] = 0.0
ax.azimuth[] = -π/2
hidedecorations!(ax)

ax = Axis3(fig[1, 3], title = "Optimized")
plt = plot_cell_data!(ax, rmesh, states_opt[step][:Temperature] .- 273.15, colorrange = (10.0, 100.0), colormap = cmap)
ax.elevation[] = 0.0
ax.azimuth[] = -π/2
hidedecorations!(ax)
Colorbar(fig[2, 1:3], plt, vertical = false)
fig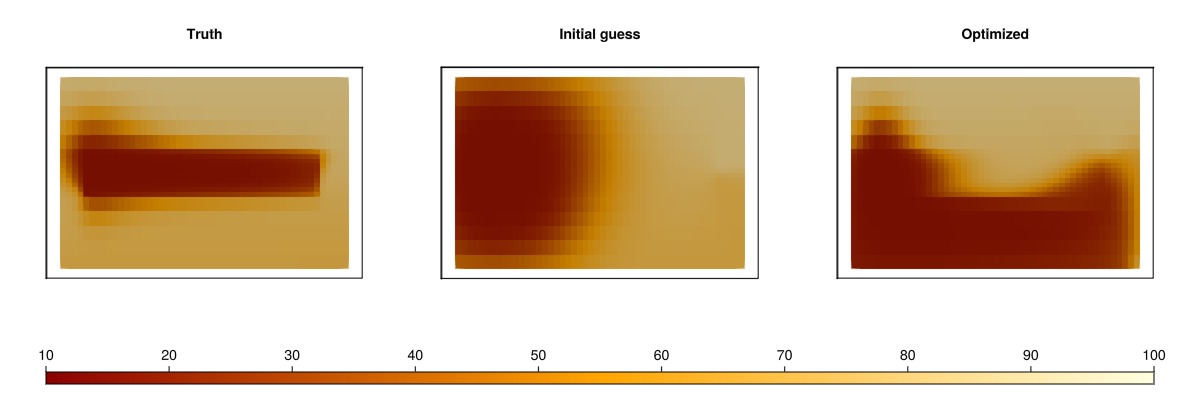

Set up control optimization

We can also use the same setup to perform control optimization, where we now can take advantage of the per-interval selection of rates and temperatures. Admittely, this problems is fairly simple, so the optimization is more conceptual than realistic: We define a new objective function that uses a fixed cost for the injected water (per degree times rate) and a similar value of produced heat. To make the optimization problem non-trivial, the cost of additional water (or higher temperature water) is significantly higher than the value of produced water with the same temperature.

temperature_injection_cost = 20.0
temperature_production_value = 8.0

function optimization_objective(m, s, dt, step_info, forces)
    T_at_prod = convert_from_si(compute_well_qoi(m, s, forces, :Producer, :temperature), :Celsius)
    T_at_inj = convert_from_si(forces[:Facility].control[:Injector].temperature, :Celsius)

    mass_rate_injector = compute_well_qoi(m, s, forces, :Injector, :mass_rate)
    mass_rate_producer = compute_well_qoi(m, s, forces, :Producer, :mass_rate)

    cost_inj = abs(mass_rate_injector) * T_at_inj * temperature_injection_cost
    value_prod = abs(mass_rate_producer) * T_at_prod * temperature_production_value
    return dt * (value_prod - cost_inj) / total_time
end

opt_ctrl = JutulDarcy.setup_reservoir_dict_optimization(prm_truth, setup_doublet_case)

DictParameters with 5 parameters (0 active), and 0 multipliers:
No active optimization parameters.
Inactive optimization parameters
┌─────────────────────────┬─────────────────────────────┬───────┬─────┬─────┐
│                    Name │ Initial value               │ Count │ Min │ Max │
├─────────────────────────┼─────────────────────────────┼───────┼─────┼─────┤
│     layer_heat_capacity │ 500.0, 600.0, 450.0         │     3 │   - │   - │
│          injection_rate │ 0.015 ± 3.47e-18            │    10 │   - │   - │
│ injection_temperature_C │ 15.0 ± 0.0                  │    10 │   - │   - │
│              layer_perm │ 9.87e-15, 7.9e-13, 1.97e-14 │     3 │   - │   - │
│        layer_porosities │ 0.1, 0.3, 0.1               │     3 │   - │   - │
└─────────────────────────┴─────────────────────────────┴───────┴─────┴─────┘
No multipliers set.

Set optimization to use injection rate and temperature

Note that as these are represented as per-interval values, we could also have passed vectors of equal length as the number of intervals for more fine-grained control over the limits. We specify that the dependencies include the whole case instead of just state0 and parameters since the forces depend on the optimization parameters.

free_optimization_parameter!(opt_ctrl, "injection_temperature_C", abs_max = 80.0, abs_min = 10.0)
free_optimization_parameter!(opt_ctrl, "injection_rate", abs_min = 1.0*liter/second, abs_max = 30.0*liter/second)

DictParameters with 5 parameters (2 active), and 0 multipliers:
Active optimization parameters
┌─────────────────────────┬──────────────────┬───────┬───────┬──────┐
│                    Name │ Initial value    │ Count │   Min │  Max │
├─────────────────────────┼──────────────────┼───────┼───────┼──────┤
│ injection_temperature_C │ 15.0 ± 0.0       │    10 │  10.0 │ 80.0 │
│          injection_rate │ 0.015 ± 3.47e-18 │    10 │ 0.001 │ 0.03 │
└─────────────────────────┴──────────────────┴───────┴───────┴──────┘
Inactive optimization parameters
┌─────────────────────┬─────────────────────────────┬───────┬─────┬─────┐
│                Name │ Initial value               │ Count │ Min │ Max │
├─────────────────────┼─────────────────────────────┼───────┼─────┼─────┤
│ layer_heat_capacity │ 500.0, 600.0, 450.0         │     3 │   - │   - │
│          layer_perm │ 9.87e-15, 7.9e-13, 1.97e-14 │     3 │   - │   - │
│    layer_porosities │ 0.1, 0.3, 0.1               │     3 │   - │   - │
└─────────────────────┴─────────────────────────────┴───────┴─────┴─────┘
No multipliers set.

Call the optimizer

prm_opt_ctrl = JutulDarcy.optimize_reservoir(opt_ctrl, optimization_objective, maximize = true, deps = :case, optimizer = :lbfgsb_qp);
opt_ctrl

DictParameters with 5 parameters (2 active), and 0 multipliers:
Active optimization parameters
┌─────────────────────────┬──────────────────┬───────┬───────┬──────┬───────────
│                    Name │ Initial value    │ Count │   Min │  Max │ Optimize ⋯
├─────────────────────────┼──────────────────┼───────┼───────┼──────┼───────────
│ injection_temperature_C │ 15.0 ± 0.0       │    10 │  10.0 │ 80.0 │ 10.8 ± 1 ⋯
│          injection_rate │ 0.015 ± 3.47e-18 │    10 │ 0.001 │ 0.03 │ 0.0157 ± ⋯
└─────────────────────────┴──────────────────┴───────┴───────┴──────┴───────────
                                                               2 columns omitted
Inactive optimization parameters
┌─────────────────────┬─────────────────────────────┬───────┬─────┬─────┐
│                Name │ Initial value               │ Count │ Min │ Max │
├─────────────────────┼─────────────────────────────┼───────┼─────┼─────┤
│ layer_heat_capacity │ 500.0, 600.0, 450.0         │     3 │   - │   - │
│          layer_perm │ 9.87e-15, 7.9e-13, 1.97e-14 │     3 │   - │   - │
│    layer_porosities │ 0.1, 0.3, 0.1               │     3 │   - │   - │
└─────────────────────┴─────────────────────────────┴───────┴─────┴─────┘
No multipliers set.

Plot the optimized injection rates and temperatures

The optimized injection rates and temperatures are plotted for each interval. The base case is shown in blue, while the optimized case is shown in orange. Note that the optimized case has reduced the injection temperature to the lower limit for all steps, and instead increase the injection rate significantly. The injection rate has a decrease part-way during the simulation, which increases the residence time of the injected water, allowing additional heat to be siphoned from the low permeable layers.

fig = Figure(size = (1200, 400))
ax = Axis(fig[1, 1], title = "Optimized injection temperature", ylabel = "Injection temperature (°C)", xlabel = "Interval")
scatter!(ax, prm_truth["injection_temperature_C"], label = "Base case")
scatter!(ax, prm_opt_ctrl["injection_temperature_C"], label = "Optimized case")
axislegend(position = :rc)

ax = Axis(fig[1, 2], title = "Optimized injection rate", ylabel = "Liter/second", xlabel = "Interval")
scatter!(ax, prm_truth["injection_rate"]./(liter/second), label = "Base case")
scatter!(ax, prm_opt_ctrl["injection_rate"]./(liter/second), label = "Optimized case")
axislegend(position = :rc)
fig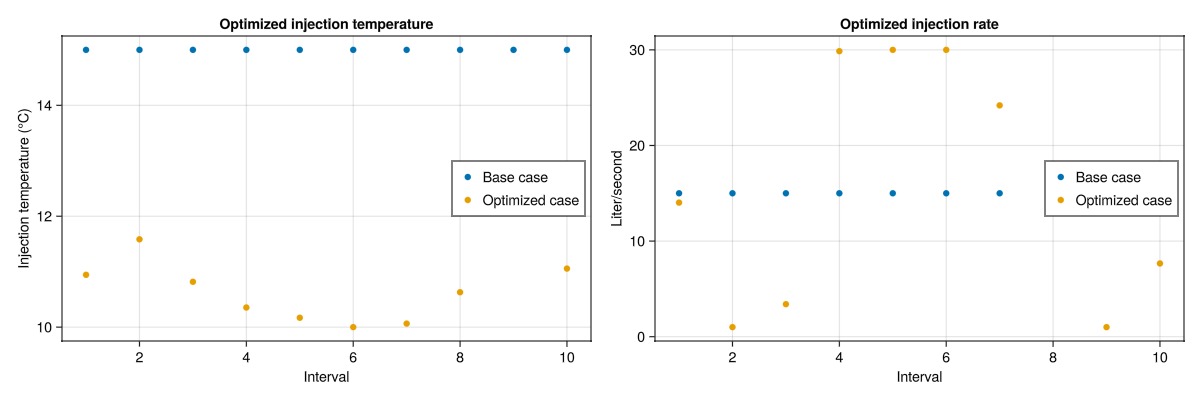

Simulate the optimized case

case_opt_ctrl = setup_doublet_case(prm_opt_ctrl)
ws_opt_ctrl, states_opt_ctrl = simulate_reservoir(case_opt_ctrl)

ReservoirSimResult with 92 entries:

  wells (2 present):
    :Producer
    :Injector
    Results per well:
       :lrat => Vector{Float64} of size (92,)
       :wrat => Vector{Float64} of size (92,)
       :temperature => Vector{Float64} of size (92,)
       :control => Vector{Symbol} of size (92,)
       :Aqueous_mass_rate => Vector{Float64} of size (92,)
       :bhp => Vector{Float64} of size (92,)
       :wcut => Vector{Float64} of size (92,)
       :mass_rate => Vector{Float64} of size (92,)
       :rate => Vector{Float64} of size (92,)
       :mrat => Vector{Float64} of size (92,)

  states (Vector with 92 entries, reservoir variables for each state)
    :Pressure => Vector{Float64} of size (1000,)
    :TotalMasses => Matrix{Float64} of size (1, 1000)
    :TotalThermalEnergy => Vector{Float64} of size (1000,)
    :FluidEnthalpy => Matrix{Float64} of size (1, 1000)
    :Temperature => Vector{Float64} of size (1000,)
    :PhaseMassDensities => Matrix{Float64} of size (1, 1000)
    :RockInternalEnergy => Vector{Float64} of size (1000,)
    :FluidInternalEnergy => Matrix{Float64} of size (1, 1000)

  time (report time for each state)
     Vector{Float64} of length 92

  result (extended states, reports)
     SimResult with 92 entries

  extra
     Dict{Any, Any} with keys :simulator, :config

  Completed at Mar. 10 2026 09:11 after 998 milliseconds, 311 microseconds, 389 nanoseconds.

Plot the distribution of temperature with and without optimization

step = 80
cmap = reverse(to_colormap(:heat))
fig = Figure(size = (1000, 400))
ax = Axis3(fig[1, 1], title = "Base case")
plot_cell_data!(ax, rmesh, states[step][:Temperature] .- 273.15, colorrange = (10.0, 100.0), colormap = cmap)
ax.elevation[] = 0.0
ax.azimuth[] = -π/2
hidedecorations!(ax)

ax = Axis3(fig[1, 2], title = "Optimized")
plt = plot_cell_data!(ax, rmesh, states_opt_ctrl[step][:Temperature] .- 273.15, colorrange = (10.0, 100.0), colormap = cmap)
ax.elevation[] = 0.0
ax.azimuth[] = -π/2
hidedecorations!(ax)
Colorbar(fig[2, 1:2], plt, vertical = false)
fig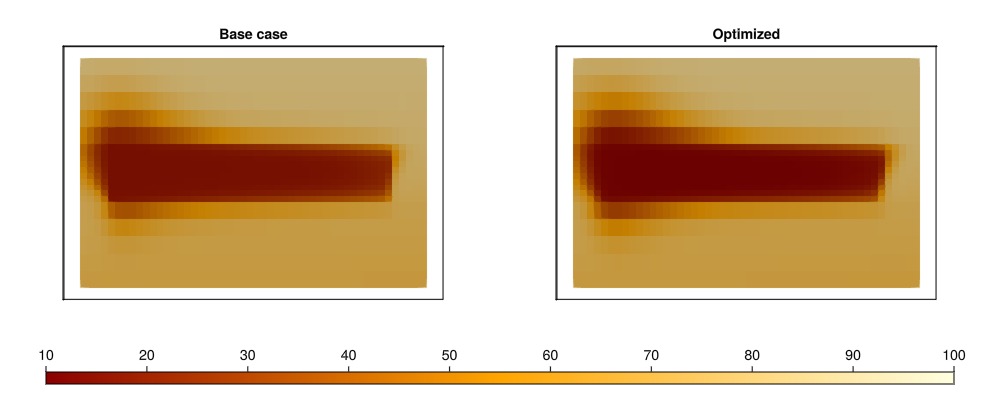

Plot the total thermal energy in the reservoir

The total thermal energy in the reservoir is computed as the sum of the thermal energy in each cell, which is the result of the rock heat capacity, porosity, fluid heat capacity and the temperature in each cell. The optimized strategy significantly decreases the remaining thermal energy in the reservoir, while still producing less cost than the base case according to our objective. The 2D nature of this problem makes it easy to recover a large amount energy, as the majority of the cells are swept by the cold front.

total_energy = map(s -> sum(s[:TotalThermalEnergy]), states)
total_energy_opt = map(s -> sum(s[:TotalThermalEnergy]), states_opt_ctrl)

fig = Figure(size = (1200, 400))
ax = Axis(fig[1, 1], title = "Total thermal energy", ylabel = "Total remaining energy (megajoules)", xlabel = "Time (days)")
t = ws.time ./ si_unit(:day)
lines!(ax, t, total_energy./1e6, label = "Base case")
lines!(ax, t, total_energy_opt./1e6, label = "Optimized case")
axislegend(position = :rc)
fig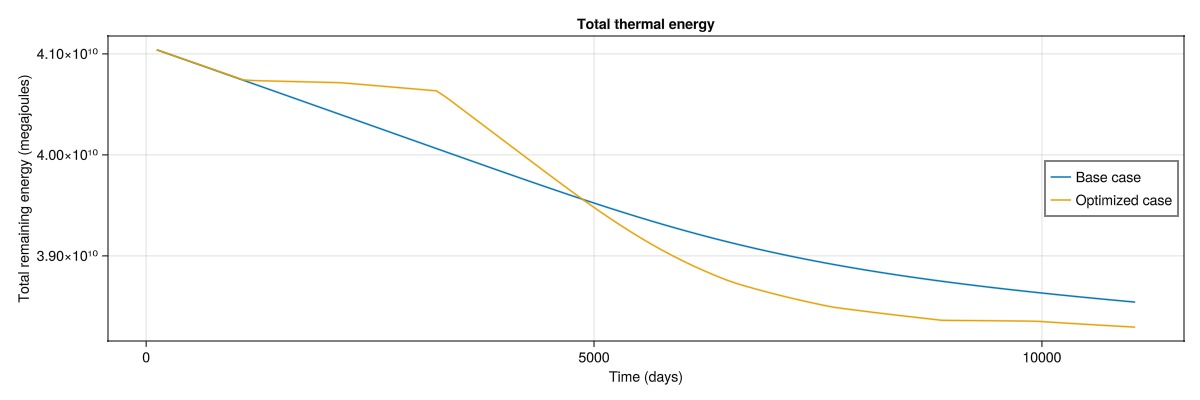

Example on GitHub

If you would like to run this example yourself, it can be downloaded from the JutulDarcy.jl GitHub repository as a script, or as a Jupyter Notebook

This example took 591.153802646 seconds to complete.

---

This page was generated using Literate.jl.