Buckley-Leverett two-phase problem
The Buckley-Leverett test problem is a classical reservoir simulation benchmark that demonstrates the nonlinear displacement process of a viscous fluid being displaced by a less viscous fluid, typically taken to be water displacing oil.
Problem definition
This is a simple model without wells, where the flow is driven by a simple source term and a simple constant pressure boundary condition at the outlet. We define a function that sets up a two-phase system, a simple 1D domain and replaces the default relative permeability functions with quadratic functions:
In addition, the phase viscosities are treated as constant parameters of 1 and 5 centipoise for the displacing and resident fluids, respectively.
The function is parametrized on the number of cells and the number of time-steps used to solve the model. This function, since it uses a relatively simple setup without wells, uses the Jutul functions directly.
using JutulDarcy, Jutul
function solve_bl(;nc = 100, time = 1.0, nstep = nc)
T = time
tstep = repeat([T/nstep], nstep)
domain = get_1d_reservoir(nc)
nc = number_of_cells(domain)
timesteps = tstep*3600*24
bar = 1e5
p0 = 100*bar
sys = ImmiscibleSystem((LiquidPhase(), VaporPhase()))
model = SimulationModel(domain, sys)
kr = BrooksCoreyRelativePermeabilities(sys, [2.0, 2.0], [0.2, 0.2])
replace_variables!(model, RelativePermeabilities = kr)
tot_time = sum(timesteps)
pv = pore_volume(domain)
irate = 500*sum(pv)/tot_time
src = SourceTerm(1, irate, fractional_flow = [1.0, 0.0])
bc = FlowBoundaryCondition(nc, p0/2)
forces = setup_forces(model, sources = src, bc = bc)
parameters = setup_parameters(model, PhaseViscosities = [1e-3, 5e-3]) # 1 and 5 cP
state0 = setup_state(model, Pressure = p0, Saturations = [0.0, 1.0])
states, report = simulate(state0, model, timesteps,
forces = forces, parameters = parameters, info_level = -1)
return states, model, report
endsolve_bl (generic function with 1 method)Run the base case
We solve a small model with 100 cells and 100 steps to serve as the baseline.
n, n_f = 100, 1000
states, model, report = solve_bl(nc = n)
print_stats(report)╭────────────────┬───────────┬───────────────┬──────────╮
│ Iteration type │ Avg/step │ Avg/ministep │ Total │
│ │ 100 steps │ 100 ministeps │ (wasted) │
├────────────────┼───────────┼───────────────┼──────────┤
│ Newton │ 3.31 │ 3.31 │ 331 (0) │
│ Linearization │ 4.31 │ 4.31 │ 431 (0) │
│ Linear solver │ 3.31 │ 3.31 │ 331 (0) │
│ Precond apply │ 0.0 │ 0.0 │ 0 (0) │
╰────────────────┴───────────┴───────────────┴──────────╯
╭───────────────┬────────┬────────────┬──────────╮
│ Timing type │ Each │ Relative │ Total │
│ │ ms │ Percentage │ ms │
├───────────────┼────────┼────────────┼──────────┤
│ Properties │ 0.0140 │ 0.66 % │ 4.6297 │
│ Equations │ 0.3412 │ 20.98 % │ 147.0744 │
│ Assembly │ 0.0067 │ 0.41 % │ 2.8830 │
│ Linear solve │ 0.1958 │ 9.24 % │ 64.7962 │
│ Linear setup │ 0.0000 │ 0.00 % │ 0.0000 │
│ Precond apply │ 0.0000 │ 0.00 % │ 0.0000 │
│ Update │ 0.0095 │ 0.45 % │ 3.1345 │
│ Convergence │ 0.0103 │ 0.63 % │ 4.4242 │
│ Input/Output │ 0.0028 │ 0.04 % │ 0.2809 │
│ Other │ 1.4312 │ 67.58 % │ 473.7169 │
├───────────────┼────────┼────────────┼──────────┤
│ Total │ 2.1176 │ 100.00 % │ 700.9398 │
╰───────────────┴────────┴────────────┴──────────╯Run refined version (1000 cells, 1000 steps)
Using a grid with 100 cells will not yield a fully converged solution. We can increase the number of cells at the cost of increasing the runtime a bit. Note that most of the time is spent in the linear solver, which uses a direct sparse LU factorization by default. For larger problems it is recommended to use an iterative solver.
states_refined, _, report_refined = solve_bl(nc = n_f);
print_stats(report_refined)╭────────────────┬────────────┬────────────────┬──────────╮
│ Iteration type │ Avg/step │ Avg/ministep │ Total │
│ │ 1000 steps │ 1000 ministeps │ (wasted) │
├────────────────┼────────────┼────────────────┼──────────┤
│ Newton │ 3.265 │ 3.265 │ 3265 (0) │
│ Linearization │ 4.265 │ 4.265 │ 4265 (0) │
│ Linear solver │ 3.265 │ 3.265 │ 3265 (0) │
│ Precond apply │ 0.0 │ 0.0 │ 0 (0) │
╰────────────────┴────────────┴────────────────┴──────────╯
╭───────────────┬────────┬────────────┬────────╮
│ Timing type │ Each │ Relative │ Total │
│ │ ms │ Percentage │ s │
├───────────────┼────────┼────────────┼────────┤
│ Properties │ 0.0686 │ 3.33 % │ 0.2239 │
│ Equations │ 0.0626 │ 3.97 % │ 0.2670 │
│ Assembly │ 0.0487 │ 3.09 % │ 0.2077 │
│ Linear solve │ 1.7707 │ 85.93 % │ 5.7814 │
│ Linear setup │ 0.0000 │ 0.00 % │ 0.0000 │
│ Precond apply │ 0.0000 │ 0.00 % │ 0.0000 │
│ Update │ 0.0212 │ 1.03 % │ 0.0694 │
│ Convergence │ 0.0137 │ 0.87 % │ 0.0586 │
│ Input/Output │ 0.0062 │ 0.09 % │ 0.0062 │
│ Other │ 0.0350 │ 1.70 % │ 0.1142 │
├───────────────┼────────┼────────────┼────────┤
│ Total │ 2.0607 │ 100.00 % │ 6.7283 │
╰───────────────┴────────┴────────────┴────────╯Plot results
We plot the saturation front for the base case at different times together with the final solution for the refined model. In this case, refining the grid by a factor 10 gave us significantly less smearing of the trailing front.
using GLMakie
x = range(0, stop = 1, length = n)
x_f = range(0, stop = 1, length = n_f)
f = Figure()
ax = Axis(f[1, 1], ylabel = "Saturation", title = "Buckley-Leverett")
for i in 1:6:length(states)
lines!(ax, x, states[i][:Saturations][1, :], color = :darkgray)
end
lines!(ax, x_f, states_refined[end][:Saturations][1, :], color = :red)
f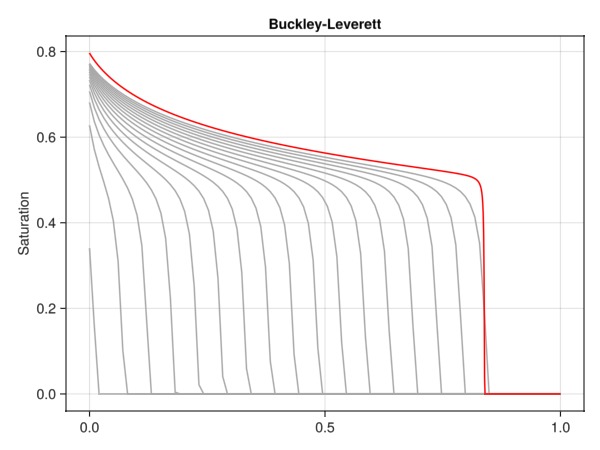
Example on GitHub
If you would like to run this example yourself, it can be downloaded from the JutulDarcy.jl GitHub repository as a script, or as a Jupyter Notebook
This page was generated using Literate.jl.