Intro to sensitivities in JutulDarcy
Sensitivites with respect to custom parameters: We demonstrate how to set up a simple conceptual model, add new parameters and variable definitions in the form of a new relative permeability function, and calculate and visualize parameter sensitivities.
We first set up a quarter-five-spot model where the domain is flooded from left to right. Some cells have lower permeability to impede flow and make the scenario more interesting.
For more details, see the paper JutulDarcy.jl - a Fully Differentiable High-Performance Reservoir Simulator Based on Automatic Differentiation.
using Jutul, JutulDarcy, GLMakie, HYPRE
darcy, kg, meter, year, day, bar = si_units(:darcy, :kilogram, :meter, :year, :day, :bar)
L = 1000.0meter
H = 100.0meter
big = false # Paper uses big, takes some more time to run
if big
nx = 500
else
nx = 100
end
dx = L/nx
g = CartesianMesh((nx, nx, 1), (L, L, H))
nc = number_of_cells(g)
perm = fill(0.1darcy, nc)
reservoir = reservoir_domain(g, permeability = 0.1darcy)
centroids = reservoir[:cell_centroids]
rock_type = fill(1, nc)
for (i, x, y) in zip(eachindex(perm), centroids[1, :], centroids[2, :])
xseg = (x > 0.2L) & (x < 0.8L) & (y > 0.75L) & (y < 0.8L)
yseg = (y > 0.2L) & (y < 0.8L) & (x > 0.75L) & (x < 0.8L)
if xseg || yseg
rock_type[i] = 2
end
xseg = (x > 0.2L) & (x < 0.55L) & (y > 0.50L) & (y < 0.55L)
yseg = (y > 0.2L) & (y < 0.55L) & (x > 0.50L) & (x < 0.55L)
if xseg || yseg
rock_type[i] = 3
end
xseg = (x > 0.2L) & (x < 0.3L) & (y > 0.25L) & (y < 0.3L)
yseg = (y > 0.2L) & (y < 0.3L) & (x > 0.25L) & (x < 0.3L)
if xseg || yseg
rock_type[i] = 4
end
end
perm = reservoir[:permeability]
@. perm[rock_type == 2] = 0.001darcy
@. perm[rock_type == 3] = 0.005darcy
@. perm[rock_type == 4] = 0.01darcy
I = setup_vertical_well(reservoir, 1, 1, name = :Injector)
P = setup_vertical_well(reservoir, nx, nx, name = :Producer)
phases = (AqueousPhase(), VaporPhase())
rhoWS, rhoGS = 1000.0kg/meter^3, 700.0kg/meter^3
system = ImmiscibleSystem(phases, reference_densities = (rhoWS, rhoGS))
model, = setup_reservoir_model(reservoir, system, wells = [I, P])
rmodel = reservoir_model(model)SimulationModel:
Model with 20000 degrees of freedom, 20000 equations and 79600 parameters
domain:
DiscretizedDomain with MinimalTPFATopology (10000 cells, 19800 faces) and discretizations for mass_flow, heat_flow
system:
ImmiscibleSystem with AqueousPhase, VaporPhase
context:
DefaultContext(BlockMajorLayout(false), 1000, 1)
formulation:
FullyImplicitFormulation()
data_domain:
DataDomain wrapping CartesianMesh (3D) with 100x100x1=10000 cells with 17 data fields added:
10000 Cells
:permeability => 10000 Vector{Float64}
:porosity => 10000 Vector{Float64}
:rock_thermal_conductivity => 10000 Vector{Float64}
:fluid_thermal_conductivity => 10000 Vector{Float64}
:rock_density => 10000 Vector{Float64}
:cell_centroids => 3×10000 Matrix{Float64}
:volumes => 10000 Vector{Float64}
19800 Faces
:neighbors => 2×19800 Matrix{Int64}
:areas => 19800 Vector{Float64}
:normals => 3×19800 Matrix{Float64}
:face_centroids => 3×19800 Matrix{Float64}
39600 HalfFaces
:half_face_cells => 39600 Vector{Int64}
:half_face_faces => 39600 Vector{Int64}
20400 BoundaryFaces
:boundary_areas => 20400 Vector{Float64}
:boundary_centroids => 3×20400 Matrix{Float64}
:boundary_normals => 3×20400 Matrix{Float64}
:boundary_neighbors => 20400 Vector{Int64}
primary_variables:
1) Pressure ∈ 10000 Cells: 1 dof each
2) Saturations ∈ 10000 Cells: 1 dof, 2 values each
secondary_variables:
1) PhaseMassDensities ∈ 10000 Cells: 2 values each
-> ConstantCompressibilityDensities as evaluator
2) TotalMasses ∈ 10000 Cells: 2 values each
-> TotalMasses as evaluator
3) RelativePermeabilities ∈ 10000 Cells: 2 values each
-> BrooksCoreyRelativePermeabilities as evaluator
4) PhaseMobilities ∈ 10000 Cells: 2 values each
-> JutulDarcy.PhaseMobilities as evaluator
5) PhaseMassMobilities ∈ 10000 Cells: 2 values each
-> JutulDarcy.PhaseMassMobilities as evaluator
parameters:
1) Transmissibilities ∈ 19800 Faces: Scalar
2) TwoPointGravityDifference ∈ 19800 Faces: Scalar
3) ConnateWater ∈ 10000 Cells: Scalar
4) PhaseViscosities ∈ 10000 Cells: 2 values each
5) FluidVolume ∈ 10000 Cells: Scalar
equations:
1) mass_conservation ∈ 10000 Cells: 2 values each
-> ConservationLaw{:TotalMasses, TwoPointPotentialFlowHardCoded{Vector{Int64}, Vector{@NamedTuple{self::Int64, other::Int64, face::Int64, face_sign::Int64}}}, Jutul.DefaultFlux, 2}
output_variables:
Pressure, Saturations, TotalMasses
extra:
OrderedCollections.OrderedDict{Symbol, Any} with keys: Symbol[]Plot the initial variable graph
We plot the default variable graph that describes how the different variables relate to each other. When we add a new parameter and property in the next section, the graph is automatically modified.
using NetworkLayout, LayeredLayouts, GraphMakie
Jutul.plot_variable_graph(rmodel)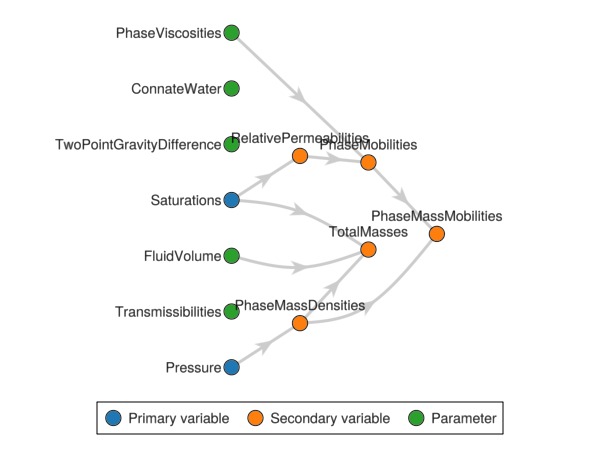
Change the variables
We replace the density variable with a more compressible version, and we also define a new relative permeability variable that depends on a new parameter KrExponents to define the exponent of the relative permeability in each cell and phase of the model.
This is done through several steps:
First, we define the type
We define functions that act on that type, in particular the update function that is used to evaluate the new relative permeability during the simulation for named inputs
SaturationsandKrExponents.We define the
KrExponentsas a model parameter with a default value, that can subsequently be used by the relative permeability.
Finally we plot the variable graph again to verify that the new relationship has been included in our model.
c = [1e-6/bar, 1e-4/bar]
density = ConstantCompressibilityDensities(p_ref = 1*bar, density_ref = [rhoWS, rhoGS], compressibility = c)
replace_variables!(rmodel, PhaseMassDensities = density);
import JutulDarcy: AbstractRelativePermeabilities, PhaseVariables
struct MyKr <: AbstractRelativePermeabilities end
@jutul_secondary function update_my_kr!(vals, def::MyKr, model, Saturations, KrExponents, cells_to_update)
for c in cells_to_update
for ph in axes(vals, 1)
S_α = max(Saturations[ph, c], 0.0)
n_α = KrExponents[ph, c]
vals[ph, c] = S_α^n_α
end
end
end
struct MyKrExp <: PhaseVariables end
Jutul.default_value(model, ::MyKrExp) = 2.0
set_parameters!(rmodel, KrExponents = MyKrExp())
replace_variables!(rmodel, RelativePermeabilities = MyKr());
Jutul.plot_variable_graph(rmodel)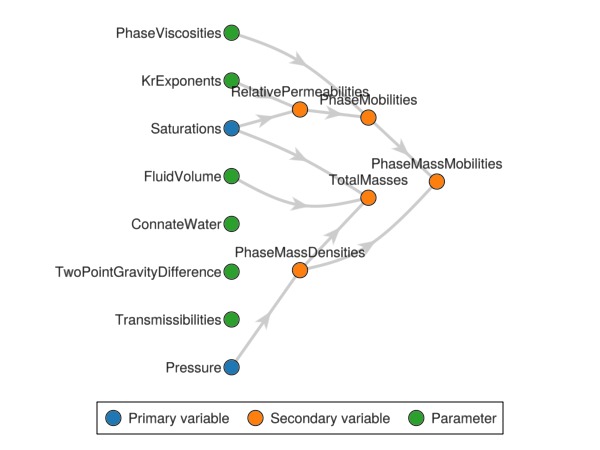
Set up scenario and simulate
parameters = setup_parameters(model)
exponents = parameters[:Reservoir][:KrExponents]
for (cell, rtype) in enumerate(rock_type)
if rtype == 1
exp_w = 2
exp_g = 3
else
exp_w = 1
exp_g = 2
end
exponents[1, cell] = exp_w
exponents[2, cell] = exp_g
end
pv = pore_volume(model, parameters)
state0 = setup_reservoir_state(model, Pressure = 150*bar, Saturations = [1.0, 0.0])
dt = repeat([30.0]*day, 12*5)
pv = pore_volume(model, parameters)
total_time = sum(dt)
inj_rate = sum(pv)/total_time
rate_target = TotalRateTarget(inj_rate)
I_ctrl = InjectorControl(rate_target, [0.0, 1.0], density = rhoGS)
bhp_target = BottomHolePressureTarget(50*bar)
P_ctrl = ProducerControl(bhp_target)
controls = Dict()
controls[:Injector] = I_ctrl
controls[:Producer] = P_ctrl
forces = setup_reservoir_forces(model, control = controls)
case = JutulCase(model, dt, forces, parameters = parameters, state0 = state0)
result = simulate_reservoir(case, output_substates = true, info_level = -1);
#
ws, states = result
ws(:Producer, :grat)Legend
┌───────┬──────────────────┬──────┬─────────────────────────┐
│ Label │ Description │ Unit │ Type of quantity │
├───────┼──────────────────┼──────┼─────────────────────────┤
│ grat │ Surface gas rate │ m³/s │ surface_volume_per_time │
└───────┴──────────────────┴──────┴─────────────────────────┘
Producer result
┌─────────┬──────────────┐
│ time │ grat │
│ days │ m³/s │
├─────────┼──────────────┤
│ 1.0 │ -0.0 │
│ 1.64286 │ -0.0 │
│ 2.05612 │ -0.0 │
│ 2.8 │ -0.0 │
│ 4.47372 │ -0.0 │
│ 7.48643 │ -0.0 │
│ 12.0055 │ -0.0 │
│ 18.7841 │ -0.0 │
│ 24.392 │ -0.0 │
│ 30.0 │ -0.0 │
│ 38.4119 │ -0.0 │
│ 49.206 │ -0.0 │
│ 60.0 │ -0.0 │
│ 73.878 │ -0.0 │
│ 90.0 │ -0.0 │
│ 105.0 │ -0.0 │
│ 120.0 │ -0.0 │
│ 135.0 │ -0.0 │
│ 150.0 │ -0.0 │
│ 165.0 │ -0.0 │
│ 180.0 │ -0.0 │
│ 195.0 │ -0.0 │
│ 210.0 │ -0.0 │
│ 225.0 │ -0.0 │
│ 240.0 │ -0.0 │
│ 255.0 │ -0.0 │
│ 270.0 │ -0.0 │
│ 285.0 │ -0.0 │
│ 300.0 │ -0.0 │
│ 315.0 │ -0.0 │
│ 330.0 │ -0.0 │
│ 345.0 │ -0.0 │
│ 360.0 │ -0.0 │
│ 375.0 │ -0.0 │
│ 390.0 │ -0.0 │
│ 405.0 │ -0.0 │
│ 420.0 │ -0.0 │
│ 435.0 │ -0.0 │
│ 450.0 │ -0.0 │
│ 465.0 │ -0.0 │
│ 480.0 │ -0.0 │
│ 495.0 │ -0.0 │
│ 510.0 │ -0.0 │
│ 525.0 │ -0.0 │
│ 540.0 │ -0.0 │
│ 555.0 │ -0.0 │
│ 570.0 │ -0.0 │
│ 585.0 │ -0.0 │
│ 600.0 │ -0.0 │
│ 615.0 │ -0.0 │
│ 630.0 │ -0.0 │
│ 645.0 │ -0.0 │
│ 660.0 │ -0.0 │
│ 675.0 │ -0.0 │
│ 690.0 │ -0.0 │
│ 705.0 │ -0.0 │
│ 720.0 │ -0.0 │
│ 735.0 │ -0.0 │
│ 750.0 │ -0.0 │
│ 765.0 │ -0.0 │
│ 780.0 │ -0.0 │
│ 795.0 │ -0.0 │
│ 810.0 │ -0.0 │
│ 825.0 │ -0.0 │
│ 840.0 │ -0.0 │
│ 855.0 │ -0.0 │
│ 870.0 │ -0.0 │
│ 885.0 │ -0.0 │
│ 900.0 │ -0.0 │
│ 915.0 │ -0.0 │
│ 930.0 │ -0.0 │
│ 945.0 │ -0.0 │
│ 960.0 │ -0.0 │
│ 975.0 │ -0.0 │
│ 990.0 │ -0.0 │
│ 1005.0 │ -0.0 │
│ 1020.0 │ -0.0 │
│ 1035.0 │ -0.0 │
│ 1050.0 │ -0.0 │
│ 1065.0 │ -0.0 │
│ 1080.0 │ -0.0 │
│ 1095.0 │ -0.0 │
│ 1110.0 │ -0.0 │
│ 1125.0 │ -0.0 │
│ 1140.0 │ -0.0 │
│ 1155.0 │ -0.0 │
│ 1170.0 │ -0.0 │
│ 1185.0 │ -0.0 │
│ 1200.0 │ -0.0 │
│ 1215.0 │ -0.0 │
│ 1230.0 │ -0.0 │
│ 1245.0 │ -0.0 │
│ 1260.0 │ -0.0 │
│ 1275.0 │ -0.0 │
│ 1290.0 │ -0.0 │
│ 1305.0 │ -0.0 │
│ 1320.0 │ -0.0 │
│ 1335.0 │ -0.0 │
│ 1350.0 │ -0.000264099 │
│ 1365.0 │ -0.00945501 │
│ 1372.5 │ -0.0156989 │
│ 1380.0 │ -0.020066 │
│ 1395.0 │ -0.0252017 │
│ 1410.0 │ -0.0286516 │
│ 1440.0 │ -0.0325127 │
│ 1470.0 │ -0.0348996 │
│ 1500.0 │ -0.0365194 │
│ 1530.0 │ -0.0377322 │
│ 1560.0 │ -0.0387128 │
│ 1590.0 │ -0.0395447 │
│ 1620.0 │ -0.040269 │
│ 1650.0 │ -0.0409083 │
│ 1680.0 │ -0.0414781 │
│ 1710.0 │ -0.0419904 │
│ 1740.0 │ -0.0424564 │
│ 1770.0 │ -0.0428874 │
│ 1800.0 │ -0.043295 │
└─────────┴──────────────┘Define objective function
We let the objective function be the amount produced of produced gas, normalized by the injected amount.
using GLMakie
function objective_function(model, state, Δt, step_i, forces)
grat = JutulDarcy.compute_well_qoi(model, state, forces, :Producer, SurfaceGasRateTarget)
return Δt*grat/(inj_rate*total_time)
end
data_domain_with_gradients = JutulDarcy.reservoir_sensitivities(case, result, objective_function, include_parameters = true)DataDomain wrapping CartesianMesh (3D) with 100x100x1=10000 cells with 23 data fields added:
10000 Cells
:permeability => 10000 Vector{Float64}
:porosity => 10000 Vector{Float64}
:rock_thermal_conductivity => 10000 Vector{Float64}
:fluid_thermal_conductivity => 10000 Vector{Float64}
:rock_density => 10000 Vector{Float64}
:cell_centroids => 3×10000 Matrix{Float64}
:volumes => 10000 Vector{Float64}
:ConnateWater => 10000 Vector{Float64}
:PhaseViscosities => 2×10000 Matrix{Float64}
:FluidVolume => 10000 Vector{Float64}
:KrExponents => 2×10000 Matrix{Float64}
19800 Faces
:neighbors => 2×19800 Matrix{Int64}
:areas => 19800 Vector{Float64}
:normals => 3×19800 Matrix{Float64}
:face_centroids => 3×19800 Matrix{Float64}
:Transmissibilities => 19800 Vector{Float64}
:TwoPointGravityDifference => 19800 Vector{Float64}
39600 HalfFaces
:half_face_cells => 39600 Vector{Int64}
:half_face_faces => 39600 Vector{Int64}
20400 BoundaryFaces
:boundary_areas => 20400 Vector{Float64}
:boundary_centroids => 3×20400 Matrix{Float64}
:boundary_normals => 3×20400 Matrix{Float64}
:boundary_neighbors => 20400 Vector{Int64}Launch interactive plotter for cell-wise gradients
plot_reservoir(data_domain_with_gradients)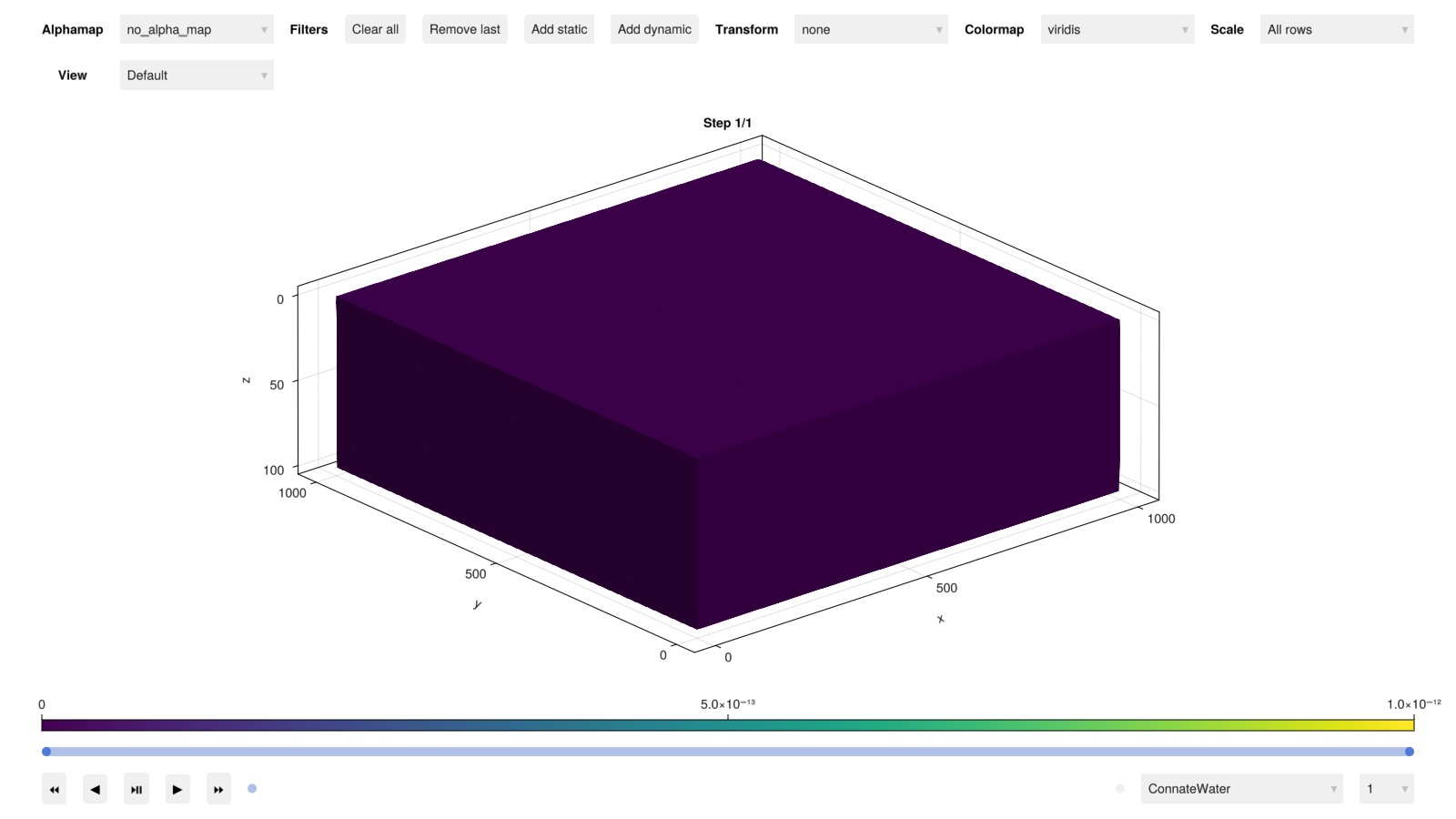
Set up plotting functions
∂K = data_domain_with_gradients[:permeability]
∂ϕ = data_domain_with_gradients[:porosity]
function get_cscale(x)
minv0, maxv0 = extrema(x)
minv = min(minv0, -maxv0)
maxv = max(maxv0, -minv0)
return (minv, maxv)
end
function myplot(title, vals; kwarg...)
fig = Figure()
myplot!(fig, 1, 1, title, vals; kwarg...)
return fig
end
function myplot!(fig, I, J, title, vals; is_grad = false, is_log = false, colorrange = missing, contourplot = false, nticks = 5, ticks = missing, colorbar = true, kwarg...)
ax = Axis(fig[I, J], title = title)
if is_grad
if ismissing(colorrange)
colorrange = get_cscale(vals)
end
cmap = :seismic
else
if ismissing(colorrange)
colorrange = extrema(vals)
end
cmap = :seaborn_icefire_gradient
end
hidedecorations!(ax)
hidespines!(ax)
arg = (; colormap = cmap, colorrange = colorrange, kwarg...)
plt = plot_cell_data!(ax, g, vals; shading = NoShading, arg...)
if colorbar
if ismissing(ticks)
ticks = range(colorrange..., nticks)
end
Colorbar(fig[I, J+1], plt, ticks = ticks, ticklabelsize = 25, size = 25)
end
return fig
endmyplot! (generic function with 1 method)Plot the permeability
myplot("Permeability", perm./darcy, colorscale = log10, ticks = [0.001, 0.01, 0.1])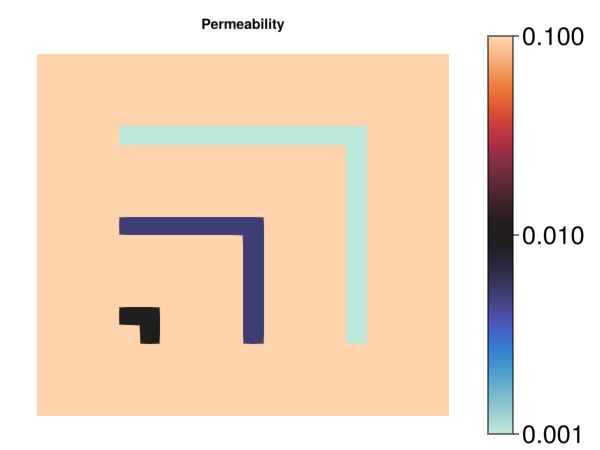
Plot the evolution of the gas saturation
fig = Figure(size = (1200, 400))
sg = states[25][:Saturations][2, :]
myplot!(fig, 1, 1, "Gas saturation", sg, colorrange = (0, 1), colorbar = false)
sg = states[70][:Saturations][2, :]
myplot!(fig, 1, 2, "Gas saturation", sg, colorrange = (0, 1), colorbar = false)
sg = states[end][:Saturations][2, :]
myplot!(fig, 1, 3, "Gas saturation", sg, colorrange = (0, 1))
fig
# ## Plot the sensitivity of the objective with respect to permeability
if big
cr = (-0.001, 0.001)
cticks = [-0.001, -0.0005, 0.0005, 0.001]
else
cr = (-0.05, 0.05)
cticks = [-0.05, -0.025, 0, 0.025, 0.05]
end
myplot("perm_sens", ∂K.*darcy, is_grad = true, ticks = cticks, colorrange = cr)
# ## Plot the sensitivity of the objective with respect to porosity
if big
cr = (-0.00001, 0.00001)
else
cr = (-0.00025, 0.00025)
end
myplot("porosity_sens", ∂ϕ, is_grad = true, colorrange = cr)
#
∂xyz = data_domain_with_gradients[:cell_centroids]
∂x = ∂xyz[1, :]
∂y = ∂xyz[2, :]
∂z = ∂xyz[3, :]
#
if big
cr = [-1e-8, 1e-8]
else
cr = [-1e-7, 1e-7]
end2-element Vector{Float64}:
-1.0e-7
1.0e-7Plot the sensitivity of the objective with respect to x cell centroids
myplot("dx_sens", ∂x, is_grad = true, colorrange = cr)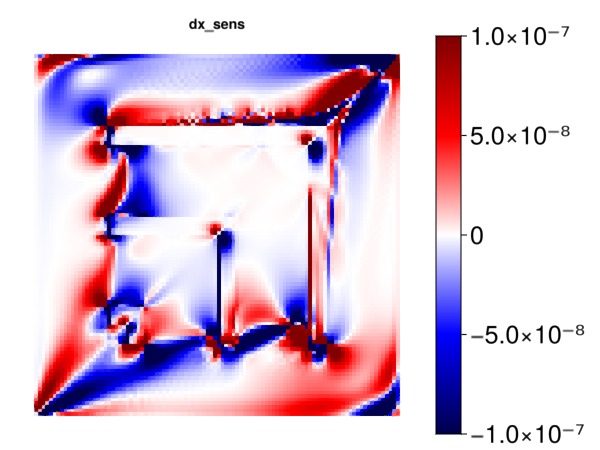
Plot the sensitivity of the objective with respect to y cell centroids
myplot("dy_sens", ∂y, is_grad = true, colorrange = cr)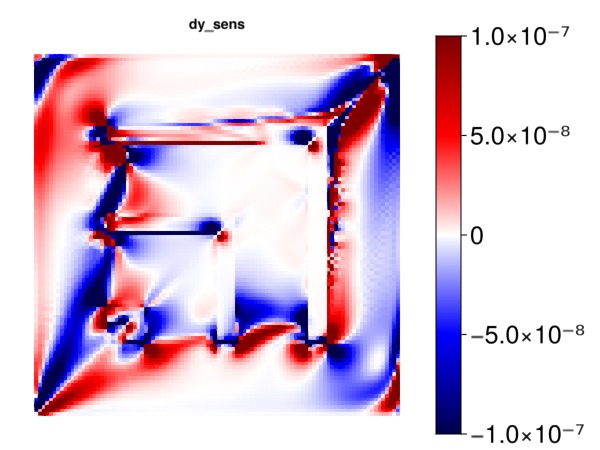
Plot the sensitivity of the objective with respect to z cell centroids
Note: The effect here is primarily coming from gravity.
myplot("dz_sens", ∂z, is_grad = true, colorrange = cr)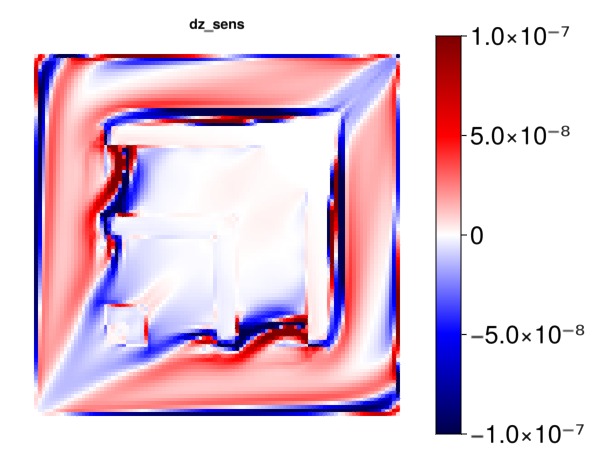
Plot the effect of the new liquid kr exponent on the gas production
if big
cr = [-1e-7, 1e-7]
else
cr = [-8e-6, 8e-6]
end
kre = data_domain_with_gradients[:KrExponents]
exp_l = kre[1, :]
myplot("exp_liquid", exp_l, is_grad = true, colorrange = cr)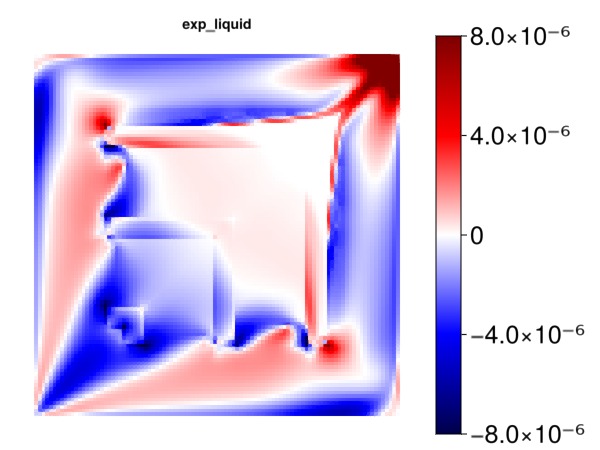
Plot the effect of the new vapor kr exponent on the gas production
exp_v = kre[2, :]
myplot("exp_vapor", exp_v, is_grad = true, colorrange = cr)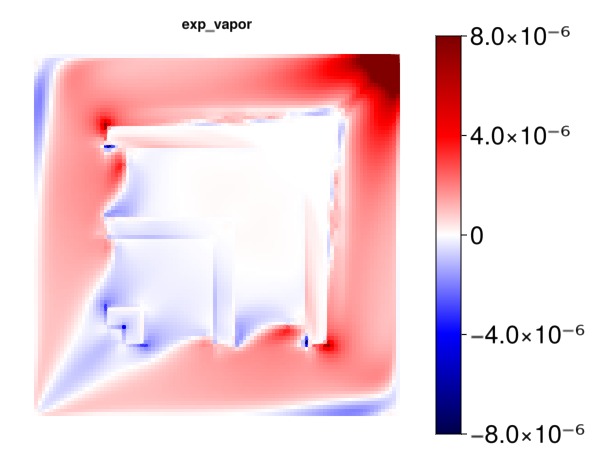
Plot the effect of the liquid phase viscosity
Note: The viscosity can in many models be a variable and not a parameter. For this simple model, however, it is treated as a parameter and we obtain sensitivities.
mu = data_domain_with_gradients[:PhaseViscosities]
if big
cr = [-0.001, 0.001]
else
cr = [-0.01, 0.01]
end
mu_l = mu[1, :]
myplot("mu_liquid", mu_l, is_grad = true, colorrange = cr)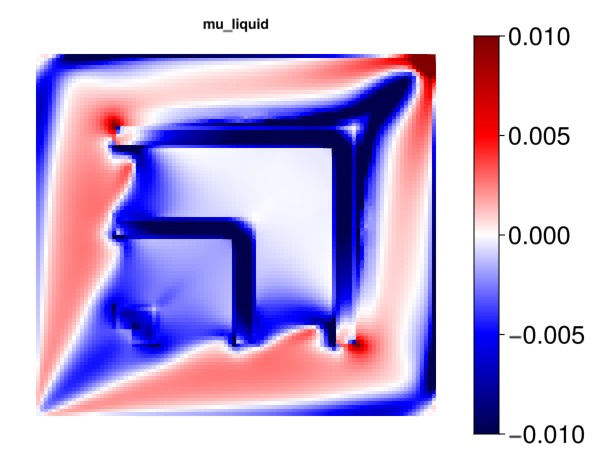
Plot the effect of the liquid phase viscosity
mu_v = mu[2, :]
myplot("mu_vapor", mu_v, is_grad = true, colorrange = cr)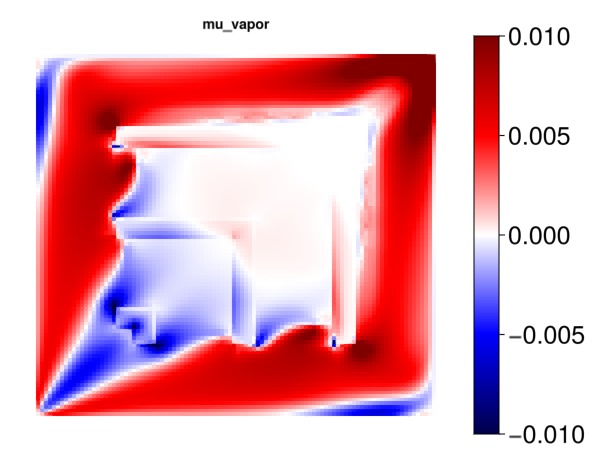
Example on GitHub
If you would like to run this example yourself, it can be downloaded from the JutulDarcy.jl GitHub repository as a script, or as a Jupyter Notebook
This page was generated using Literate.jl.